
【题目】如图所示,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成.
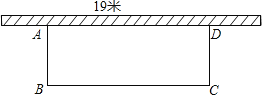
(1)若围成的面积为180m,试求出自行车车棚的长和宽;
(2)能围成的面积为200m自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
【答案】(1)10米,18米 (2)答案见解析
【解析】
(1)设AB=x,则BC=38﹣2x,根据围成的面积为180m列出方程,求出x的值,根据题意取舍即可;
(2)根据题意列出方程,整理得x-19x+100=0,利用根的判别式确定方程是否有根即可解答.
(1)解:设AB=x,则BC=38﹣2x;
根据题意列方程的,x(38﹣2x)=180,
解得x1=10,x2=9;
当x=10, 38-2x=18(米),
当x=9, 38-2x=20(米),不合题意舍去,
答:若围成的面积为180m,自行车车棚的长和宽分别为10米,18米。
(2) 解:根据题意列方程的,x(38﹣2x)=200,
整理得出:x-19x+100=0;
△=b-4ac=361-400=-39<0,
故此方程没有实数根,
答:因此如果墙长19m,满足条件的花园面积不能达到200m。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有当
有最小值是1,只有当![]() 时,才能得到这个式子的最小值1.
时,才能得到这个式子的最小值1.
同样![]() ,因此
,因此![]() 有最大值是8,只有当
有最大值是8,只有当![]() 时,才能得到这个式子的最大值8.
时,才能得到这个式子的最大值8.
(1)当x= 时,代数式﹣2(x﹣3)2+5有最大值为 .
(2)当x= 时,代数式2x2+4x+3有最小值为 .
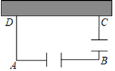
(3)矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
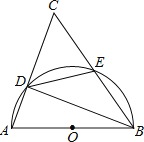
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
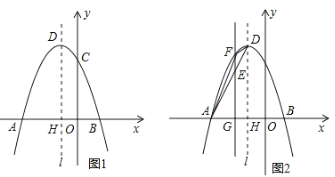
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
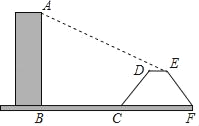
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com