
【题目】某学校计划组织500人参加社会实践活动,与某公交公司接洽后,得知该公司有A,B型两种客车,它们的载客量和租金如表所示:

经测算,租用A,B型客车共13辆较为合理,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的代数式填写下表:

(2)采用怎样的租车方案可以使总的租车费用最低,最低为多少?
【答案】(1)28(13﹣x);250(13﹣x);(2)租A型车8辆、B型车5辆时,总的租车费用最低,最低为4450元.
【解析】(1)设租用A型客车x辆,则租用B型客车(13﹣x)辆,B型车的载客量28(13﹣x),租金为250(13﹣x).
故答案为:28(13﹣x);250(13﹣x).
(2)设租车的总费用为W元,则有:W=400x+250(13﹣x)=150x+3250.
由已知得:45x+28(13﹣x)≥500,解得:x≥8.
∵在W=150x+3250中150>0,∴当x=8时,W取最小值,最小值为4450元.
故租A型车8辆、B型车5辆时,总的租车费用最低,最低为4450元.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元,相关资料表明:甲、乙两种鱼苗的成活率为80%,90%
(1)若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?
(2)若要使这批鱼苗的总成活率不低于85%,则乙种鱼苗至少购买多少条?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等社团活动项目(每人只限一项)的情况,并将所得数据进行了统计,结果如图所示.![]()
![]()
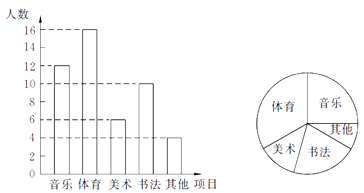
(1)在这次调查中,一共抽查了多少名学生?
(2)求出扇形统计图中参加“音乐”活动项目在扇形统计图中所对扇形圆心角的度数.
(3)若该校有2 400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1000元,乙货船每艘运费1200元.
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式;
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com