
【题目】如图,点M是线段AB中点,AD、BC交于点N,连接AC、BD、MC、MD,∠l=∠2,∠3=∠4.
(1)求证:△AMD≌△BMC;
(2)图中在不添加新的字母的情况下,请写出除了“△AMD≌△BMC”以外的所有全等三角形,并选出其中一对进行证明.

【答案】(1)详见解析;(2)△AMC≌△BMD,△ABC≌△BAD,△ACN≌△BDN.
【解析】
(1)根据ASA即可判断;(2)全等三角形有:△AMC≌△BMD,△ABC≌△BAD,△ACN≌△BDN.根据三角形全等的判定方法一一判断即可.
(1)∵点M是AB中点,
∴AM=BM,
∵∠1=∠2,
∴∠AMD=∠BMC,
在△AMD和△BMC中,
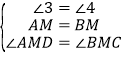 ,
,
∴△AMD≌△MBC(ASA);
(2)△AMC≌△BMD,△ABC≌△BAD,△ACN≌△BDN.
理由:∵△AMD≌△MBC,
∴AD=BC,
∵∠3=∠4,AB=BA,
∴△BAD≌△ABC(SAS),
∴AC=BD,∠BDN=∠ACN,
∵∠ANC=∠BND,
∴△ANC≌△BND(AAS),
∵AC=BD,∠CAM=∠DBM,AM=BM,
∴△AMC≌△BMD(SAS).


科目:初中数学 来源: 题型:
【题目】在春运期间,宁波火车站加大了安检力度,原来在北广场执勤的有10人,在南广场执勤的有6人,现调50人去支援.设调往北广场x人.
(1)则南广场增援后有执勤多少人(用含x的代数式表示).
(2)若要使在北广场执勤人数是在南广场执勤人数的2倍,问应调往北广场、南广场两处各多少人?
(3)通过适当的调配支援人数,使在北广场执勤人数恰好是在南广场执勤人数的n倍(n是大于1的正整数,不包括1).求符合条件的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= ![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
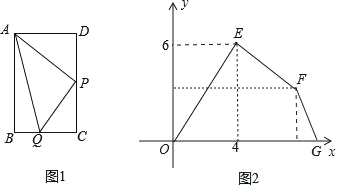
【题目】如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知图①中抛物线y=ax2+bx+c经过点D(﹣1,0)、C(0,﹣1)、E(1,0).
(1)求图①中抛物线的函数表达式; 
(2)将图①中抛物线向上平移一个单位,再绕原点O顺时针旋转180°后得到图②中抛物线,则图②中抛物线的函数表达式为; 
(3)图②中抛物线与直线y=﹣ ![]() x﹣
x﹣ ![]() 相交于A、B两点(点A在点B的左侧),如图③,求点A、B的坐标,并直接写出当一次函数的值大于二次函数的值时,x的取值范围.
相交于A、B两点(点A在点B的左侧),如图③,求点A、B的坐标,并直接写出当一次函数的值大于二次函数的值时,x的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示. 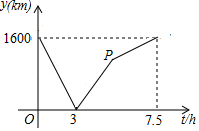
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
查看答案和解析>>
科目:初中数学 来源: 题型:
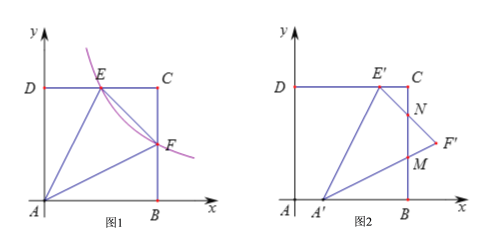
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com