
【题目】四边形ABCD中,∠A=140°,∠D=80°.
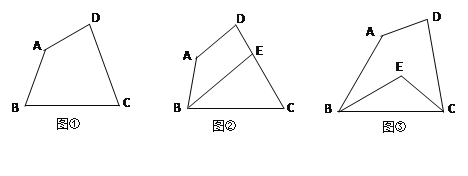
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【答案】(1)70°;(2)60°;(3)110°
【解析】
(1)根据四边形的内角和是360°,结合已知条件就可求解;
(2)根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,进一步根据四边形的内角和定理进行求解;
(3)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数.
(1)在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°, 又∠A=140°,∠D=80°,∠B=∠C,
∴140°+∠C+∠C+80°=360°,即∠C=70°.
(2)∵BE∥AD,∠A=140°,∠D=80°,
∴∠BEC=∠D,∠A+∠ABE=180°.
∴∠BEC=80°,∠ABE=40°.
∵BE是∠ABC的平分线,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
(3)在四边形ABCD中, 有∠A+∠ABC+∠BCD+∠D=360°, ∠A=140°,∠D=80°,
所以∠ABC+∠BCD=140°,从而有![]() ∠ABC+
∠ABC+![]() ∠BCD=70°.
∠BCD=70°.
因为∠ABC和∠BCD的角平分线交于点E,所以有∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD.
∠BCD.
故∠C=180°-(∠EBC +∠ECB)=180°-(![]() ∠ABC+
∠ABC+![]() ∠BCD)=180°-70°=110°.
∠BCD)=180°-70°=110°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )

A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
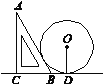
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com