
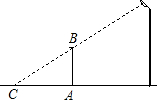
 如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④. 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC、△DEF和△GMN都是等边三角形,且点E、M在线段AC上,点G在线段EF上,那么∠1+∠2+∠3等于( )
如图,△ABC、△DEF和△GMN都是等边三角形,且点E、M在线段AC上,点G在线段EF上,那么∠1+∠2+∠3等于( )| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一只蚂蚁从A点沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
如图,一只蚂蚁从A点沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题.
如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF、BF,EF与对角线AC交于点O,且BE=BF,∠DFE=2∠ACF.
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EF、BF,EF与对角线AC交于点O,且BE=BF,∠DFE=2∠ACF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com