【题目】如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为100° 的菱形，剪口与折痕所成的角的度数应为（ ）
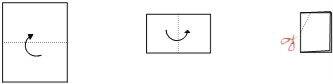
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
科目：初中数学 来源： 题型：
【题目】如图，在 Rt△ABC 中，∠ABC=90°，AB=BC=
，将△ABC 绕点 C 逆时针旋转 60°，得到△MNC， 连接 BM，则 BM 的长是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
在数学课上，老师提出如下问题：
尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．
已知线段a，c如图．
小芸的作法如下：
①取AB=c，作AB的垂直平分线交AB于点O；
②以点O为圆心，OB长为半径画圆；
③以点B为圆心，a长为半径画弧，与⊙O交于点C；
④连接BC，AC．
则Rt△ABC即为所求．
老师说：“小芸的作法正确．”
请回答：小芸的作法中判断∠ACB是直角的依据是 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若关于x的方程4（2﹣x）+x=ax的解为正整数，且关于x的不等式组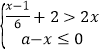
有解，则满足条件的所有整数a的值之和是（ ）
A. 4 B. 0 C. ﹣1 D. ﹣3
查看答案和解析>>
科目：初中数学 来源： 题型：
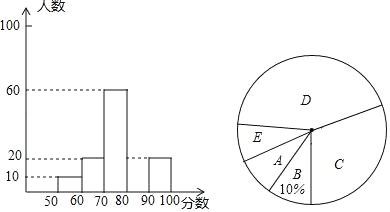
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周，某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况，统计结果后绘制了如图的两副不完整的统计图，请结合图中相关数据回答下列问题：
A | 50＜n≤60 |
B | 60＜n≤70 |
C | 70＜n≤80 |
D | 80＜n≤90 |
E | 90＜n≤100 |
（1）本次调查的总人数为 人，在扇形统计图中“C”所在扇形的圆心角的度数为 度；
（2）补全频数分布图；
（3）若在这一周里，该路口共有7000人通过，请估计得分超过80的大约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设x是实数，现在我们用{x}表示不小于x的最小整数，如{3.2}=4，{﹣2.6}=﹣2，{4}=4，{﹣5}=5．在此规定下任一实数都能写出如下形式：x={x}﹣b，其中0≤b＜1．
（1）直接写出{x}与x，x+1的大小关系是 （由小到大）；
（2）根据（1）中的关系式解决下列问题：
①求满足{3x+11}=6的x的取值范围；
②解方程：{3.5x+2}=2x﹣
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数a、b，定义一种运算“
”为：ab=a2 +ab－2，有下列命题：
①13=2；
②方程x1=0的根为：x1 =－2，x2 =1；
③不等式组 
的解集为：－1＜x＜4；
④点（
，
）在函数y=x（－1）的图象上．
其中正确的是（ ）
A. ①②③④ B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）．现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；
（总费用＝广告赞助费+门票费）
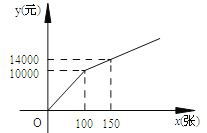
方案二：购买门票方式如图所示．
解答下列问题：
（1）方案一中，y与x的函数关系式为 ；
方案二中，当0≤x≤100时，y与x的函数关系式为 ，
当x＞100时，y与x的函数关系式为 ；
（2）如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；
（3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是线段AB上任一点，AB＝12 cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2 cm/s，D点的运动速度为3 cm/s，运动的时间为t s.
(1)若AP＝8 cm.
①运动1 s后，求CD的长；
②当D在线段PB运动上时，试说明AC＝2CD；
(2)如果t＝2 s时，CD＝1 cm，试探索AP的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
