
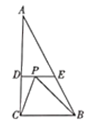
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一动点.过点
内一动点.过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() 为等腰三角形,且
为等腰三角形,且![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】1或![]()
【解析】
分以下三种情况:①若BP=CP,过点P作PF⊥BC于点F,有DP=CF=![]() BC;②若BP=BC,过点P作PF⊥BC于点F,则在Rt△BPF中先求出BF的长,从而根据DP=CF可得出DP的长;③若BC=CP,由勾股定理以及相似三角形的判定与性质分别求出DP,DE的长,此时DP>DE,此种情况不存在.综上可得出结果.
BC;②若BP=BC,过点P作PF⊥BC于点F,则在Rt△BPF中先求出BF的长,从而根据DP=CF可得出DP的长;③若BC=CP,由勾股定理以及相似三角形的判定与性质分别求出DP,DE的长,此时DP>DE,此种情况不存在.综上可得出结果.
解:∵∠ACB=90°,PD⊥AC,
∴DE∥BC.
∴![]() ,
,
又BC=5,∴CD=3.
分以下三种情况:
①若BP=CP,如图1,过点P作PF⊥BC于F,
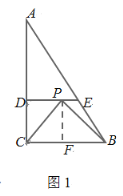
则四边形CDPF为矩形,
∴DP=CF,
又CP=BP,PF⊥BC,
∴CF=BF=![]() BC=
BC=![]() ,
,
∴DP=CF=![]() ;
;
②若BP=BC=5,如图2,过点P作PF⊥BC于F,
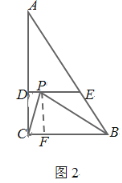
则四边形CDPF为矩形,
∴PF=CD=3,
在Rt△BPF中,由勾股定理可得BF=4,
∴CF=BC-BF=1,
∴DP=1;
③若BC=CP=5,如图3,
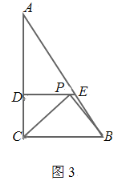
则在Rt△CDP中,根据勾股定理得,DP=4,
又DE∥BC,
∴△ADE∽△ACB,
∴![]() ,
,
∴![]() ,∴DE=
,∴DE=![]() ,
,
此时DP>DE,不符合题意.
综上所述,PD的长为1或![]() .
.
故答案为:1或![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
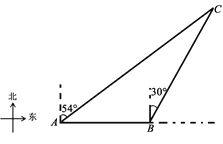
【题目】我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,再航行一段距离到达
方向,再航行一段距离到达![]() 处,测得小岛
处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与山东舰相距
方向,且与山东舰相距![]() 海里。求山东舰从
海里。求山东舰从![]() 到
到![]() 航行了多少海里?(精确到
航行了多少海里?(精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
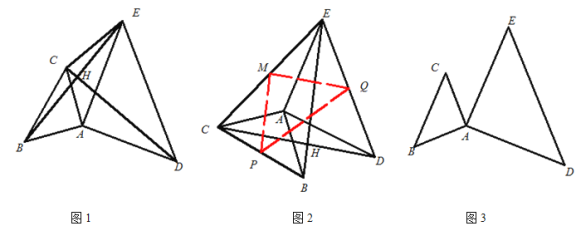
【题目】已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中AB=AC,AD=AE,
∠BAC=90°,∠DAE=90°.
(1)观察猜想
如图1,连接BE、CD交于点H,再连接CE,那么BE和CD的数量关系和位置关系分别是
(2)探究证明
将图1中的△ABC绕点A逆时针旋转到图2的位置时,分别取BC、CE、DE的中点P、M、Q,连接MP、PQ、MQ,请判断MP和MQ的数量关系和位置关系,并说明理由;
(3)拓展延伸
已知AB=![]() ,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
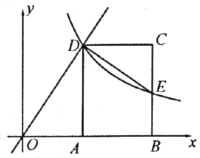
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在直线
在直线![]() 位于第一象限的图像上,反比例函数
位于第一象限的图像上,反比例函数![]() 的图像经过点
的图像经过点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
(1)如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
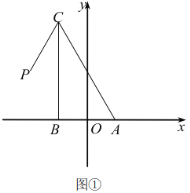
【题目】在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 在第二象限,点
在第二象限,点![]() .
.
(1)如图①,求![]() 点坐标及
点坐标及![]() 的大小;
的大小;
(2)将![]() 绕
绕![]() 点逆时针旋转得到
点逆时针旋转得到![]() ,点
,点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() 为
为![]() 的面积.
的面积.
①如图②,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
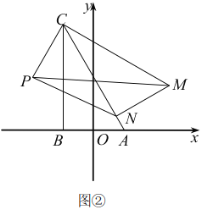
②求![]() 的取值范围(直接写出结果即可)
的取值范围(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生平均每天的课外学习时间情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学习时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.

请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了____名学生,并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在____等级内;
(3)表示B等级的扇形圆心角α的度数是_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测得某建筑物的高度![]() ,在
,在![]() 处用高为
处用高为![]() 米的测角仪
米的测角仪![]() ,测得该建筑物顶端
,测得该建筑物顶端![]() 的仰角为
的仰角为![]() ,再向建筑物方向前进
,再向建筑物方向前进![]() 米,又测得该建筑物顶端
米,又测得该建筑物顶端![]() 的仰角为
的仰角为![]() .
.
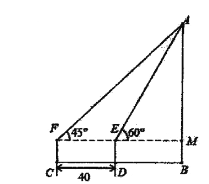
(1)填空:![]() ,
,![]() ;
;
(2)求该建筑物的高度![]() .(结果保留根号)
.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com