
分析 (1)由题意知,第一组第n个数为(-1)n+1,第二组第n个数为(-1)n•2n,第三组第n个数为n2,据此得出两组的第100个数即可得答案;
(2)根据以上规律,先找到每组数列的第10个数,继而可得答案.
解答 解:(1)根据题意知,第三组的第100个数是1002=10000,
第二组的第100个数是2×100=200,
∴10000÷200=50,
即第三组的第100个数是第二组的第100个数的50倍,
故答案为:50;
(2)∵第一组第10个数为-1,第二组第10个数为2×10=20,第三组第10个数为102=100,
∴这三个数的和为119.
点评 本题主要考查数字的变化规律,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-b,a) | B. | (-a,b) | C. | (1-b,a+1) | D. | (-1,-b+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
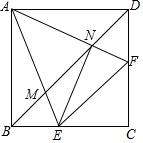 如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN
如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com