
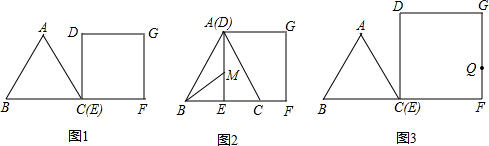
分析 (1)分两种情况利用三角形的面积公式可以表示出:当$0≤t<2\sqrt{3}$时,重叠部分的面积$S=\frac{\sqrt{3}}{2}{t}^{2}$,当$2\sqrt{3}≤t≤6$时,用△ABC的面积-△BEH的面积即可求出重叠部分的面积;
(2)当点A与点D重合时,得出$BE=CE=2\sqrt{3}$,再由条件可以求出AN的值,分三种情况讨论求出EH的值,①AN=AH=4时,②AN=NH=4时,此时H点在线段AG的延长线上,③AH=NH时,此时H点为线段AG的中垂线与AG的交点,从而可以求出答案.
(3)在运动中当0≤t<2时,如图2,△PEC∽△EFQ,可以得出t值;当2≤t≤4时,如图3,△PEC∽△QDF,可以得出t值.
解答 解:(1)当$0≤t<2\sqrt{3}$时,如图1:
∵△ABC为等边三角形,
∴∠HCE=60°.
∴$\frac{EH}{EC}=\sqrt{3}$.
∴EC=t,EH=$\sqrt{3}t$.
∴∴△HEC的面积=$\frac{1}{2}EC•EH=\frac{1}{2}×t×\sqrt{3}t=\frac{\sqrt{3}}{2}{t}^{2}$,
即:$S=\frac{\sqrt{3}}{2}{t}^{2}$,
当$2\sqrt{3}≤t≤6$时,如图2所示: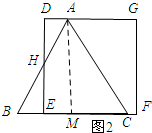
过点A作AM⊥BC,垂足为M.
当2$\sqrt{3}$≤t≤6时,EC=t,则BE=4$\sqrt{3}$-t,
∵△ABC为等边三角形,
∴∠B=60°.
∴$\frac{HE}{BE}=\sqrt{3}$.
∴HE=$\sqrt{3}$BE,即EH=$\sqrt{3}$.
∴△BHE的面积=$\frac{1}{2}EH•BE=\frac{1}{2}×\sqrt{3}×(4\sqrt{3}-t)^{2}$,
∴AM=6.
∴△ABC的面积=$\frac{1}{2}CB•AM=\frac{1}{2}×4\sqrt{3}×6=12\sqrt{3}$.
∴重合部分的面积=S△ABC-S△BHE=$-\frac{\sqrt{3}}{2}{t}^{2}+12t-12\sqrt{3}$.
即:$S=-\frac{\sqrt{3}}{2}{t}^{2}+12t-12\sqrt{3}$.
(2)当点A与点D重合时,$BE=CE=2\sqrt{3}$,
∵BM平分∠ABE,
∴$∠MBE=\frac{1}{2}∠ABE=30°$,
∴ME=2,
∵∠ABM=∠BAM,
∴AM=BM=4,
∵△ABM≌△ACN,
∴∠CAN=30°,AN=4
①AN=AH=4时,$EH=\sqrt{A{E}^{2}+A{H}^{2}}=2\sqrt{13}$,
②AN=NH=4时,此时H点在线段AG的延长线上,
∵H点不在在线段AG上,
∴舍去,
③AH=NH时,此时H点为线段AN的中垂线与AG的交点,如图3,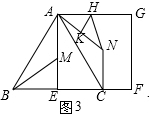
∴$AK=\frac{1}{2}AN=2$,$AH=\frac{AK}{cos∠HAK}=\frac{4\sqrt{3}}{3}$,
∴$EH=\sqrt{A{E}^{2}+A{H}^{2}}=\frac{2\sqrt{93}}{3}$.
(3)当0≤t<2时,如图4,
△PEC∽△EFQ,
∴$\frac{PE}{EF}=\frac{EC}{QF}$,
∴$\frac{3t}{4\sqrt{3}}=\frac{\sqrt{3}t}{2\sqrt{3}t}$,
∴$t=\frac{2\sqrt{3}}{3}$,
当2≤t≤4时,如图3,△PEC∽△QDE,
∴$\frac{PE}{DQ}=\frac{EC}{DE}$,
∴$\frac{12-3t}{8\sqrt{3}-2\sqrt{3}t}=\frac{\sqrt{3}t}{4\sqrt{3}}$,
∴$\sqrt{3}{t}^{2}-(6+4\sqrt{3})t+24=0$,
∴$(\sqrt{3}t-6)(t-4)=0$,
∴t1=4,${t}_{2}=2\sqrt{3}$.
点评 本题考查了求函数的解析式,正方形的性质,全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质,勾股定理的运用,根据题意画出符合题意的图形是解答本题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
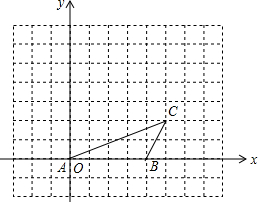 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com