
【题目】反比例函数 ![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数 ![]() 的图象于点M , △AOM的面积为3.
的图象于点M , △AOM的面积为3.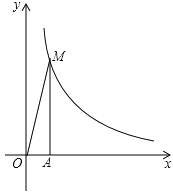
(1)求反比例函数的解析式;
(2)设点B的坐标为(t , 0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上,求t的值.
的图象上,求t的值.
【答案】
(1)
解答:∵△AOM的面积为3,
∴ ![]() |k|=3,
|k|=3,
而k>0,
∴k=6,
∴反比例函数解析式为 ![]() ;
;
(2)
解答:当以AB为一边的正方形ABCD的顶点D在反比例函数 ![]() 的图象上,则D点与M点重合,即AB=AM,
的图象上,则D点与M点重合,即AB=AM,
把x=1代 ![]() 得y=6,
得y=6,
∴M点坐标为(1,6),
∴AB=AM=6,
∴t=1+6=7;
当以AB为一边的正方形ABCD的顶点C在反比例函数 ![]() 的图象上,
的图象上,
则AB=BC=t-1,
∴C点坐标为(t,t-1),
∴t(t-1)=6,
整理为 ![]() -t-6=0,解得
-t-6=0,解得 ![]() =3,
=3, ![]() =-2(舍去),
=-2(舍去),
∴t=3,
∴以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上时,t的值为7或3.
的图象上时,t的值为7或3.
【解析】根据反比例函数k的几何意义得到 ![]() |k|=3,得到满足条件的k=6,从而得到反比例函数解析式为
|k|=3,得到满足条件的k=6,从而得到反比例函数解析式为 ![]() ;(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数
;(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数 ![]() 的图象上,则D点与M点重合,即AB=AM , 再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数
的图象上,则D点与M点重合,即AB=AM , 再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数 ![]() 的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t , t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.
的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t , t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.


科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
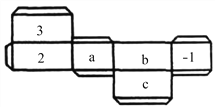
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点A(-1, ![]() )、B(1,
)、B(1, ![]() )、C(2,
)、C(2, ![]() )是反比例函数
)是反比例函数 ![]() 图象上的三个点,则下列结论正确的是( )
图象上的三个点,则下列结论正确的是( )
A.![]() >
> ![]() >
> ![]()
B.![]() >
> ![]() >
> ![]()
C.![]() >
> ![]() >
> ![]()
D.![]() >
> ![]() >
> ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x>0时,反比例函数 ![]() ( )
( )
A.图象在第四象限,y随x的增大而增大
B.图象在第三象限,y随x的增大而增大
C.图象在第二象限,y随x的增大而减小
D.图象在第一象限,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组,某天乘一辆汽车检修东西走向的“汉施公路”时,约定向东行驶为正,向西行驶为负,他们从A地出发到收工时的行走记录为(单位:千米):-4,+7,-9,+8,+6,-5,+10,-8.
(1)收工时,该小组距离A地多远?
(2) 若汽车行驶每千米耗油0.2升,那么从A地出发到回到A地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CA⊥BA
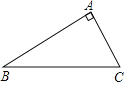
(1)画图:①延长BA到D,使AD=BA,连接CD;
②过点A画AE∥BC,AE与CD相交于点E;
③过点B画BF⊥CD,交DC的延长线于点F.
思考:图中有______条线段,它们的长度表示点到直线的距离;
(2)度量:
①你度量的哪些量?______;
②通过度量你发现:______.(写一条发现即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com