
| A. | 55 | B. | 57 | C. | 69 | D. | 71 |
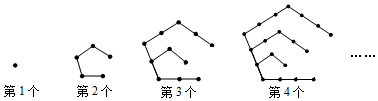
分析 根据图形可知:第一个图形有1枚棋子,第二个图形有1+4=5枚棋子,第三个图形有1+4+6=11枚棋子,第四个图形有1+4+6+8=19枚棋子,…,根据数的变化可找出变化规律“第n个图形有n2+n-1枚棋子”,依此规律即可得出结论.
解答 解:∵第一个图形有1枚棋子,第二个图形有1+4=5枚棋子,第三个图形有1+4+6=11枚棋子,第四个图形有1+4+6+8=19枚棋子,…,
∴第n个图形有1+4+6+…+2n=(2+n)(n-1)+1=n2+n-1枚棋子.
当n=7时,n2+n-1=72+7-1=55.
故选A.
点评 本题考查了规律型中图形的变化类,根据图形中棋子数目的变化找出变化规律“第n个图形有n2+n-1枚棋子”是解题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 20 | D. | 16或20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com