
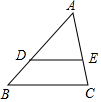 如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且DE=$\frac{2}{3}$BC.
如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且DE=$\frac{2}{3}$BC.分析 (1)根据相似三角形的判定与性质,可得AE的长,根据线段的和差,可得答案;
(2)根据相似三角形的判定与性质,可得AE,AD的长,根据向量的减法运算,可得答案.
解答 解:(1)由DE∥BC,得
△ADE∽△ABC,$\frac{AE}{AC}$=$\frac{DE}{BC}$.
又DE=$\frac{2}{3}$BC且AC=6,得
AE=$\frac{2}{3}$AC=4,
CE=AC-AE=6-4=2;
(2)如图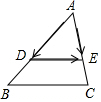 ,
,
由DE∥BC,得
△ADE∽△ABC,$\frac{AE}{AC}$=$\frac{DE}{BC}$.
又AC=6且DE=$\frac{2}{3}$BC,得
AE=$\frac{2}{3}$AC,AD=$\frac{2}{3}$AB.
$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AC}$=$\frac{2}{3}$$\overrightarrow{b}$,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$=$\frac{2}{3}$$\overrightarrow{b}$.
$\overrightarrow{DE}$=$\overrightarrow{AE}$-$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.
点评 本题考查了向量的运算,利用向量的减法运算是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
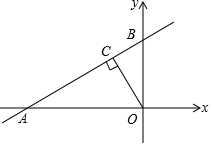 如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).
如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 画一个三角形其内角和为361° | |
| B. | 任意做一个矩形,其对角线相等 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow a$的模为3 | B. | $\overrightarrow a$与$\overrightarrow b$的模之比为-3:1 | ||
| C. | $\overrightarrow a$与$\overrightarrow b$平行且方向相同 | D. | $\overrightarrow a$与$\overrightarrow b$平行且方向相反 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com