
分析 先估算出$\sqrt{5}$和$\sqrt{13}$的范围,求出a、b的值,再代入求出即可.
解答 解:∵2<$\sqrt{5}$<3,3<$\sqrt{13}$<4,
∴a=$\sqrt{5}$-2,b=$\sqrt{13}$-3,
∴a2-($\sqrt{5}$+2)a-$\sqrt{13}$b+3
=($\sqrt{5}$-2)2-($\sqrt{5}$+2)($\sqrt{5}$-2)-$\sqrt{13}$×($\sqrt{13}$-3)+3
=5-4$\sqrt{5}$+4-5+4-13+3$\sqrt{13}$+3
=-2-4$\sqrt{5}$+3$\sqrt{13}$.
点评 本题考查了估算无理数的大小,能求出a、b的值是解此题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
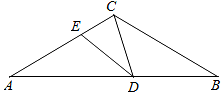 如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com