
【题目】(1)(问题解决)已知点![]() 在
在![]() 内,过点
内,过点![]() 分别作关于
分别作关于![]() 、
、![]() 的对称点
的对称点![]() 、
、![]() .
.
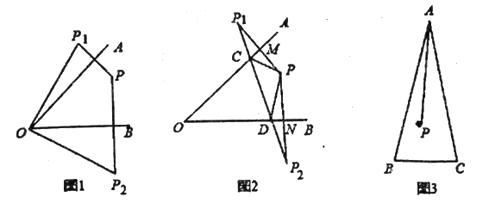
①如图1,若![]() ,请直接写出
,请直接写出![]() ______;
______;
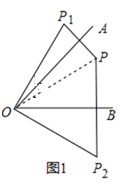
②如图2,连接![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③在②的条件下,若![]() 度(
度(![]() ),请直接写出
),请直接写出![]() ______度(用含
______度(用含![]() 的代数式表示).
的代数式表示).
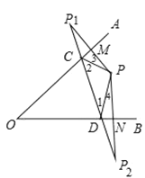
(2)(拓展延伸)利用“有一个角是![]() 的等腰三角形是等边三角形”这个结论,解答问题:如图3,在
的等腰三角形是等边三角形”这个结论,解答问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内部一定点,
内部一定点,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,请你在图3中画出使
上,请你在图3中画出使![]() 周长最小的点
周长最小的点![]() 、
、![]() 的位置(不写画法),并直接写出
的位置(不写画法),并直接写出![]() 周长的最小值.
周长的最小值.
【答案】(1)【问题解决】①![]() ;②
;②![]() ;③
;③![]() ;(2)【拓展延伸】如图,见解析;
;(2)【拓展延伸】如图,见解析;![]() 周长最小值为8.
周长最小值为8.
【解析】
(1)①连接OP,由点P关于直线OA的对称点![]() ,点P关于直线OB的对称点
,点P关于直线OB的对称点![]() ,可得
,可得![]()
![]() ,
,![]()
![]() ,再由
,再由![]()
![]()
![]() +
+![]()
![]() =2(
=2(![]() +
+![]() )=2
)=2![]() ,即可求得∠AOB的度数;②由
,即可求得∠AOB的度数;②由![]() ,根据三角形的内角和定理可得
,根据三角形的内角和定理可得![]() ;由轴对称的性质得,
;由轴对称的性质得,![]() ,
,![]() ,再由三角形外角的性质可得
,再由三角形外角的性质可得![]() ,
,![]() ,所以
,所以![]() ,即可求得
,即可求得![]() ;由轴对称的性质可得
;由轴对称的性质可得![]() ,由四边形的内角和为360°即可求得
,由四边形的内角和为360°即可求得![]() ; ③类比②的方法即可解答;(2)作点P关于边AB的对称点
; ③类比②的方法即可解答;(2)作点P关于边AB的对称点![]() ,再作点P关于边AC的对称点
,再作点P关于边AC的对称点![]() ,连结
,连结![]()
![]() ,分别交AB、AC于点E、F,此时
,分别交AB、AC于点E、F,此时![]() 的周长最小,最小为
的周长最小,最小为![]()
![]() 的长,由①的方法求得∠
的长,由①的方法求得∠![]() A
A![]() =60°,
=60°,![]() A=
A=![]() A,再由“有一个角是
A,再由“有一个角是![]() 的等腰三角形是等边三角形”即可判定△
的等腰三角形是等边三角形”即可判定△![]() A
A![]() 是等边三角形,根据等边三角形的性质可得
是等边三角形,根据等边三角形的性质可得![]()
![]() =AP=8,由此即可得
=AP=8,由此即可得![]() 周长最小值为8.
周长最小值为8.
(1)①连接OP,
∵点P关于直线OA的对称点![]() ,点P关于直线OB的对称点
,点P关于直线OB的对称点![]() ,
,
∴![]()
![]() ,
,![]()
![]() ,
,
∴![]()
![]()
![]() +
+![]()
![]() =2(
=2(![]() +
+![]() )=2
)=2![]() ,
,
故答案为:50°;
②如图2,
∵![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,
∴![]() ;
;
③![]() .
.
如图2,
∵![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,
∴![]() =
=![]() ;
;
故答案为:![]() ;
;
(2)如图所示,![]() 的周长最小,周长最小值为8.
的周长最小,周长最小值为8.

①画点P关于边AB的对称点![]() ,
,
②画点P关于边AC的对称点![]() ,
,
③连结![]()
![]() ,分别交AB、AC于点E、F,
,分别交AB、AC于点E、F,
此时![]() 的周长最小,周长最小值为8.
的周长最小,周长最小值为8.


科目:初中数学 来源: 题型:
【题目】某工艺品每件的成本是50元,在某段时间内若以每件x元出售,可卖出(200-2x)件,设这段时间内售出该工艺品的利润为y元.
(1)直接写出利润y(元)与售价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果要使利润不低于1200元,且成本不超过2500元,请直接写出x的范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.
(1)求甲、乙每天能生产多少万只口罩?
(2)问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
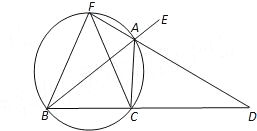
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
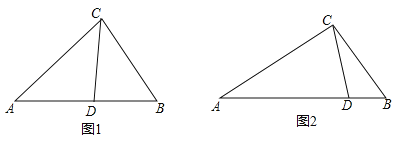
查看答案和解析>>
科目:初中数学 来源: 题型:
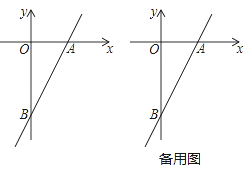
【题目】已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A,B,点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2.
(1)当P为线段AB的中点时,d1+d2=_____;
(2)设点P横坐标为m,用含m的代数式表示d1+d2,并求当d1+d2=3时点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com