
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µć A£Ø©2£¬0£©£¬B£Ø2£¬0£©£¬C£Ø0£¬2£©£¬µć D£¬µćE·Ö±šŹĒ AC£¬BCµÄÖŠµć£¬½«”÷CDEČʵćCÄꏱÕėŠż×ŖµĆµ½”÷CD”äE”䣬¼°Šż×Ŗ½ĒĪŖ¦Į£¬Į¬½Ó AD”䣬BE”䣮
£Ø1£©ČēĶ¼¢Ł£¬Čō 0”ć£¼¦Į£¼90”ć£¬µ± AD”ä”ĪCE”䏱£¬Ēó¦ĮµÄ“󊔣»
£Ø2£©ČēĶ¼¢Ś£¬Čō 90”ć£¼¦Į£¼180”ć£¬µ±µć D”äĀäŌŚĻ߶Ī BE”äÉĻŹ±£¬Ēó sin”ĻCBE”äµÄÖµ£»
£Ø3£©ČōÖ±ĻßAD”äÓėÖ±ĻßBE”äĻą½»ÓŚµćP£¬ĒóµćPµÄŗį×ų±źmµÄȔֵ·¶Ī§£ØÖ±½ÓŠ“³ö½į¹ū¼“æÉ£©£®

”¾“š°ø”æ£Ø1£©60”ć£»£Ø2£©![]() £»£Ø3£©©
£»£Ø3£©©![]() ”Üm”Ü
”Üm”Ü![]() £®
£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ(1)ČēĶ¼1ÖŠ£¬øł¾ŻĘ½ŠŠĻߵĊŌÖŹæɵƔĻAD”äC=”ĻE”äCD”ä=90”ć£¬ŌŁøł¾ŻAC=2CD”䣬ĶĘ³ö”ĻCAD”ä=30”ć£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£» (2)ČēĶ¼2ÖŠ£¬×÷CK”ĶBE”äÓŚK£®øł¾Ż¹“¹É¶ØĄķŗĶµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹĒó³öCKµÄ³¤£¬ŌŁøł¾Żsin”ĻCBE”ä= ![]() £¬¼“æɽā¾öĪŹĢā£»(3)øł¾ŻĶ¼3”¢Ķ¼4·Ö±šĒó³öµćPŗį×ų±źµÄ×ī“óÖµŅŌ¼°×īŠ”Öµ¼“æɽā¾öĪŹĢā.
£¬¼“æɽā¾öĪŹĢā£»(3)øł¾ŻĶ¼3”¢Ķ¼4·Ö±šĒó³öµćPŗį×ų±źµÄ×ī“óÖµŅŌ¼°×īŠ”Öµ¼“æɽā¾öĪŹĢā.
ŹŌĢā½āĪö£ŗ
£Ø1£©ČēĶ¼1ÖŠ£¬
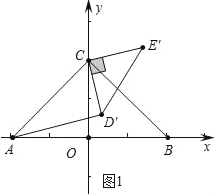
”ßAD”ä”ĪCE”䣬
”ą”ĻAD”äC=”ĻE”äCD”ä=90”ć£¬
”ßAC=2CD”䣬
”ą”ĻCAD”ä=30”ć£¬
”ą”ĻACD”ä=90”ć©”ĻCAD”ä=60”ć£¬
”ą¦Į=60”ć£®
£Ø2£©ČēĶ¼2ÖŠ£¬×÷CK”ĶBE”äÓŚK£®
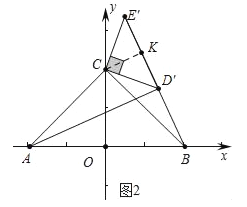
ӧAC=BC= ![]() =2
=2 ![]() £¬
£¬
”ąCD”ä=CE”ä= ![]() £¬
£¬
”ß”÷CD”äE”äŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬CD”ä=CE”ä= ![]() £¬
£¬
”ąD”äE”ä=2£¬
”ßCK”ĶD”äE”䣬
”ąKD”ä=E”äK£¬
”ąCK= ![]() D”äE”ä=1£¬
D”äE”ä=1£¬
”ąsin”ĻCBE”ä= ![]() =
= ![]() =
= ![]() £®
£®
£Ø3£©ČēĶ¼3ÖŠ£¬ŅŌCĪŖŌ²ŠÄ![]() ĪŖ°ė¾¶×÷”ŃC£¬µ±BE”äÓė”ŃCĻąĒŠŹ±AP×ī³¤£¬ŌņĖıߊĪCD”äPE”äŹĒÕż·½ŠĪ£¬×÷PH”ĶABÓŚH£®
ĪŖ°ė¾¶×÷”ŃC£¬µ±BE”äÓė”ŃCĻąĒŠŹ±AP×ī³¤£¬ŌņĖıߊĪCD”äPE”äŹĒÕż·½ŠĪ£¬×÷PH”ĶABÓŚH£®
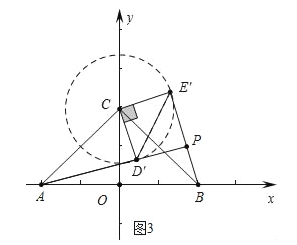
ӧAP=ADӊ+PDӊ= ![]() +
+ ![]() £¬
£¬
”ßcos”ĻPAB= ![]() =
= ![]() £¬
£¬
”ąAH=2+ ![]() £¬
£¬
”ąµćPŗį×ų±źµÄ×ī“óÖµĪŖ![]() £®
£®
ČēĶ¼4ÖŠ£¬µ±BE”äÓė”ŃCĻąĒŠŹ±AP×ī¶Ģ£¬ŌņĖıߊĪCD”äPE”äŹĒÕż·½ŠĪ£¬×÷PH”ĶABÓŚH£®
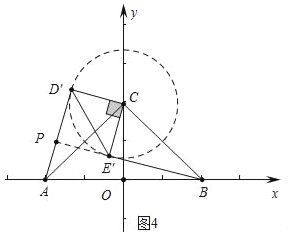
øł¾Ż¶Ō³ĘŠŌæÉÖŖOH= ![]() £¬
£¬
”ąµćPŗį×ų±źµÄ×īŠ”ÖµĪŖ©![]() £¬
£¬
”ąµćPŗį×ų±źµÄȔֵ·¶Ī§ĪŖ©![]() ”Üm”Ü
”Üm”Ü![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ČōÖ±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬ĒŅĮ½ĢõÖ±ĻßÓė
£¬ĒŅĮ½ĢõÖ±ĻßÓė![]() Öį·Ö±š½»ÓŚµć
Öį·Ö±š½»ÓŚµć![]() ”¢µć
”¢µć![]() £»ÄĒĆ“
£»ÄĒĆ“![]() µÄĆ껿ĪŖ____£®
µÄĆ껿ĪŖ____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬EF”ĪAD£¬AD”ĪBC£¬CEĘ½·Ö”ĻBCF£¬”ĻDAC=115”ć£¬”ĻACF=25”ć£¬Ōņ”ĻFEC=_____.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖׄה¼Æ°²¹ś¼Ź·ćŅ¶ĀĆÓĪ½ŚµÄÉĢ»ś£¬Ä³ÉĢµź¾ö¶Ø¹ŗ½ųA”¢BĮ½ÖÖĀĆÓĪ¼ĶÄīĘ·.Čō¹ŗ½ųAÖÖ¼ĶÄīĘ·8¼ž£¬BÖÖ¼ĶÄīĘ·3¼ž£¬ŠčŅŖ950ŌŖ£»Čō¹ŗ½ųAÖÖ¼ĶÄīĘ·5¼ž£¬BÖÖ¼ĶÄīĘ·6¼ž£¬ŠčŅŖ800ŌŖ.
£Ø1£©Ēó¹ŗ½ųA”¢BĮ½ÖÖ¼ĶÄīĘ·Ć漞ø÷Šč¶ąÉŁŌŖ£»
£Ø2£©ČōøĆÉĢµź¾ö¶Ø¹ŗ½ųÕāĮ½ÖÖ¼ĶÄīĘ·¹²100¼ž£¬æ¼ĀĒŹŠ³”ŠčĒóŗĶ׏½šÖÜ×Ŗ£¬ÓĆÓŚ¹ŗĀņÕā100¼ž¼ĶÄīĘ·µÄ׏½š²»ÉŁÓŚ7500ŌŖ£¬µ«²»³¬¹ż7650ŌŖ£¬ÄĒĆ“øĆÉĢµź¹²ÓŠ¼øÖÖ½ų»õ·½°ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC£½90”ć£¬”ĻB£½30”ć£¬ŅŌAĪŖŌ²ŠÄ£¬ČĪŅā³¤ĪŖ°ė¾¶»»”·Ö±š½»AB”¢ACÓŚµćMŗĶN£¬ŌŁ·Ö±šŅŌM”¢NĪŖŌ²ŠÄ£¬“óÓŚ![]() MNµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćP£¬Į¬½ÓAP£¬²¢Ķ¢³¤½»BCÓŚµćD£¬ŌņĻĀĮŠĖµ·ØÖŠÕżČ·µÄøöŹżŹĒ£Ø””””£©
MNµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćP£¬Į¬½ÓAP£¬²¢Ķ¢³¤½»BCÓŚµćD£¬ŌņĻĀĮŠĖµ·ØÖŠÕżČ·µÄøöŹżŹĒ£Ø””””£©
¢ŁADŹĒ”ĻBACµÄĘ½·ÖĻß
¢Ś”ĻADC£½60”ć
¢ŪµćDŌŚABµÄ“¹Ö±Ę½·ÖĻßÉĻ
¢ÜČōAD£½2dm£¬ŌņµćDµ½ABµÄ¾ąĄėŹĒ1dm
¢ŻS”÷DAC£ŗS”÷DAB£½1£ŗ2

A.2B.3C.4D.5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒŅŃ¾Ń§¹ż½«Ņ»øö¶ąĻīŹ½·Ö½āŅņŹ½µÄ·½·ØÓŠĢį¹«ŅņŹ½·ØŗĶŌĖÓĆ¹«Ź½·Ø£¬Ę䏵·Ö½āŅņŹ½µÄ·½·Ø»¹ÓŠ·Ö×é·Ö½ā·Ø”¢²šĻī·Ø”¢×ÖĻą³Ė·ØµČµČ£¬½«Ņ»øö¶ąĻīŹ½ŹŹµ±·Ö×éŗó£¬æÉĢį¹«ŅņŹ½»ņŌĖÓĆ¹«Ź½¼ĢŠų·Ö½āµÄ·½·Ø½Š×ö·Ö×é·Ö½ā£®
ĄżČē£ŗ![]()
ĄūÓĆÕāÖÖ·Ö×éµÄĖ¼Ļė·½·Ø½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©·Ö½āŅņŹ½![]() £»
£»
£Ø2£©![]() Čż±ßa£¬b£¬cĀś×ć
Čż±ßa£¬b£¬cĀś×ć![]() ÅŠ¶Ļ
ÅŠ¶Ļ![]() µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³Ń§Ļ°Š”×éŌŚĢ½Ė÷”°ø÷ÄŚ½Ē¶¼ĻąµČµÄŌ²ÄŚ½Ó¶ą±ßŠĪŹĒ·ńĪŖÕż¶ą±ßŠĪ”±Ź±£¬½ųŠŠČēĻĀĢÖĀŪ£ŗ
¼×Ķ¬Ń§£ŗÕāÖÖ¶ą±ßŠĪ²»Ņ»¶ØŹĒÕż¶ą±ßŠĪ£¬ČēŌ²ÄŚ½Ó¾ŲŠĪ£®
ŅŅĶ¬Ń§£ŗĪŅ·¢ĻֱߏżŹĒ6Ź±£¬ĖüŅ²²»Ņ»¶ØŹĒÕż¶ą±ßŠĪ£¬ČēĶ¼1£¬”÷ABCŹĒÕżČż½ĒŠĪ£¬ ![]() £¬Ö¤Ć÷Įł±ßŠĪADBECFµÄø÷ÄŚ½ĒĻąµČ£¬µ«ĖüĪ“±ŲŹĒÕżĮł±ßŠĪ£®
£¬Ö¤Ć÷Įł±ßŠĪADBECFµÄø÷ÄŚ½ĒĻąµČ£¬µ«ĖüĪ“±ŲŹĒÕżĮł±ßŠĪ£®
±ūĶ¬Ń§£ŗĪŅÄÜÖ¤Ć÷£¬±ßŹżŹĒ5Ź±£¬ĖüŹĒÕż¶ą±ßŠĪ£¬ĪŅĻė”£¬±ßŹżŹĒ7Ź±£¬ĖüæÉÄÜŅ²ŹĒÕż¶ą±ßŠĪ£®
£Ø1£©ĒėÄćĖµĆ÷ŅŅĶ¬Ń§¹¹ŌģµÄĮł±ßŠĪø÷ÄŚ½ĒĻąµČ£»
£Ø2£©ĒėÄćÖ¤Ć÷£¬ø÷ÄŚ½Ē¶¼ĻąµČµÄŌ²ÄŚ½ÓĘ߱ߊĪABCDEFG£ØČēĶ¼2£©ŹĒÕżĘ߱ߊĪ£»£Ø²»±ŲŠ“ŅŃÖŖ£¬ĒóÖ¤£©
£Ø3£©øł¾ŻŅŌÉĻĢ½Ė÷¹ż³Ģ£¬Ģį³öÄćµÄ²ĀĻė£®£Ø²»±ŲÖ¤Ć÷£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖĮĖ½āĘßÄź¼¶800Ćūѧɜʌ֊ŹżŃ§æ¼ŹŌĒéæö£¬“ÓÖŠ³éČ”ĮĖ100ĆūѧɜµÄŹżŃ§³É¼Ø½ųŠŠĮĖĶ³¼Ę£®ĻĀĆę5øöÅŠ¶ĻÖŠÕżČ·µÄÓŠ£Ø””””£©
¢ŁÕāÖÖµ÷²é·½Ź½ŹĒ³éŃłµ÷²é£»¢Ś800ĆūѧɜŹĒ×ÜĢå£ŗ¢ŪĆæĆūѧɜµÄŹżŃ§³É¼ØŹĒøöĢå¢Ü100ĆūѧɜŹĒ×ÜĢåµÄŅ»øöŃł±¾£»¢ŻŃł±¾ČŻĮæŹĒ100
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABEÖŠ£¬”ĻAEB=90”ć£¬µćFŹĒ±ßAEÉĻµÄŅ»µć£¬DŹĒEFµÄÖŠµć£¬¹żµćF×÷BEµÄĘ½ŠŠĻß½»BDµÄŃÓ³¤ĻßÓŚµćC£®ČōCF=AF£¬BE=6cm£¬DE=3cm£¬Ēó”÷ABCµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com