
【题目】如图,在△ABC中,D是BC边上的一点,过A点作BC的平行线,截取AE=BD,连结EB,连结EC交AD于点F.
(1)证明:当点F是AD的中点时,点D是BC的中点;
(2)证明:当点D是AB的中垂线与BC的交点时,四边形AEBD是菱形.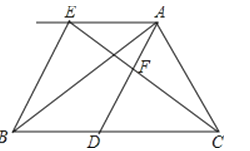
【答案】证明:(1)∵AE∥BC,
∴∠EAF=∠CDF,
又∵F是AD的中点,
∴AF=DF,
∴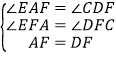
∴△EAF≌△CDF,
∴DC=AE,
∵AE=BD,
∴BD=DC;
(2)∵AE=BD且AE∥BD,
∴四边形AEBD是平行四边形,
又∵点D是AB的中垂线与BC的交点,则有BD=AD,
∴平行四边形AEBD一组邻边相等,
∴四边形AEBD是菱形.
【解析】(1)证得△EAF≌△CDF后即可得到DC=AE,然后根据AE=BD得到BD=DC;
(2)首先利用一组对边相等且平行的四边形为平行四边形证得平行四边形,然后根据中垂线的性质得到BD=AD,从而利用邻边相等的平行四边形是菱形进行判定即可.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形).


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
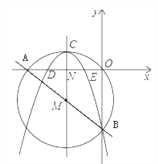
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )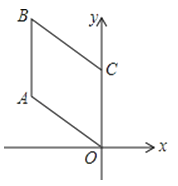
A.(﹣2,2+![]() )
)
B.(2,2+![]() )
)
C.(-![]() , 2+
, 2+![]() )
)
D.(![]() , 2+
, 2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A.三角形的内心到三角形三个顶点的距离相等B.重心有可能在三角形外
C.外心是三角形三条角平分线的交点D.等边三角形的内心与外心重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B分别是![]() 轴、
轴、![]() 轴上的动点,点C、D是某个函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。例如:如图,正方形ABCD是一次函数
轴上的动点,点C、D是某个函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。例如:如图,正方形ABCD是一次函数![]() 图像的其中一个伴侣正方形
图像的其中一个伴侣正方形
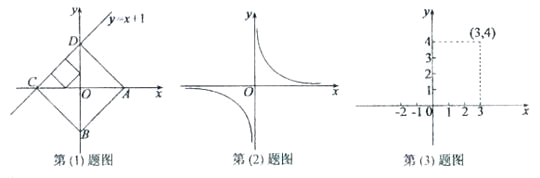
(1)若某函数是一次函数![]() ,求它的图像的所有伴侣正方形的边长;
,求它的图像的所有伴侣正方形的边长;
(2)若某函数是反比例函数![]() ,他的图像的伴侣正方形为ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
,他的图像的伴侣正方形为ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
(3)若某函数是二次函数![]() ,它的图像的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标
,它的图像的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标![]() ,写出符合题意的其中一条抛物线解析式
,写出符合题意的其中一条抛物线解析式![]() ,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?
,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?![]() 。(本小题只需直接写出答案)
。(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过“乘方”和“开方”运算,下面给同学们介绍一种新的运算,即对数运算.
定义:如果ab=N(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作logaN=b.
例如:因为![]() ,所以
,所以![]() ;因为
;因为![]() ,所以
,所以![]() .
.
(1)填空: ![]() _____,
_____, ![]() ________.
________.
(2)如果![]() ,求m的值.
,求m的值.
(3)对于“对数”运算,小明同学认为有“![]() ”,他的说法正确吗?如果正确,请给出证明过程;如果不正确,请说明理由,并加以改正。
”,他的说法正确吗?如果正确,请给出证明过程;如果不正确,请说明理由,并加以改正。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com