
【题目】把一副三角板的直角顶点O重叠在一起,
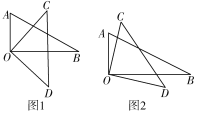
(1)如图1,当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图2,当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
(3)当∠BOC的余角的4倍等于∠AOD时,则∠BOC是多少度?
【答案】(1)180°;(2)180°;(3)60°.
【解析】
试题(1)根据平分线的性质分别求出∠BOC和∠BOD的度数,然后求出∠AOD+∠BOC的度数;(2)、当不平分时可得∠AOD+∠BOC=∠AOB+∠COD求出答案;(3)结合前面两个可得∠AOD=180°-∠BOC=4(90°-∠BOC),求出∠BOC的度数.
试题解析:(1)当OB平分∠COD时,有∠BOC=∠BOD=45°,
于是∠AOC=90°-45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+ ∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=∠AOB+∠COD,
∴∠AOD+∠BOC=90°+90°=180°.
(3)由上得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC, 180°-∠BOC=4(90°-∠BOC),
∴∠BOC=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD. 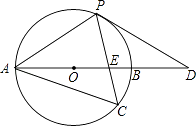
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若 ![]() :
: ![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
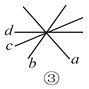
【题目】观察下列图形,寻找对顶角(不含平角).
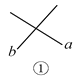
(1)如图①,图中共有____对对顶角;
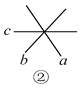
(2)如图②,图中共有____对对顶角;
(3)如图③,图中共有____对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角对数的关系,猜想:若有n条直线相交于一点,则共可形成__________对对顶角;
(5)若有180条直线相交于一点,则可形成________对对顶角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( ) 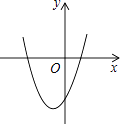
A.y1<y2
B.y1>y2
C.y的最小值是﹣3
D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”; 王华同学说: “第三边长是![]() .” 还有一些同学也提出了不同的看法……
.” 还有一些同学也提出了不同的看法……
(1)假如你也在课堂上, 你的意见如何? 为什么?
(2)通过上面数学问题的讨论, 你有什么感受? (用一句话表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形). 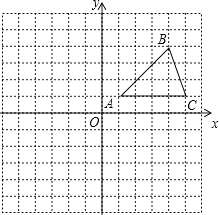
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2 , 并直接写出点B2、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地,如图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题:
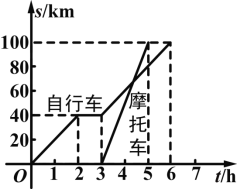
(1)甲地与乙地相距多少千米?两人分别用了几个小时才到达乙地?谁先到达乙地?先到者早到多长时间?
(2)分别描述在这个过程中自行车和摩托车的行驶状态;
(3)求摩托车行驶的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位篮球运动员跳起投篮,球沿抛物线y=﹣ ![]() x2+3.5运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
x2+3.5运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米. 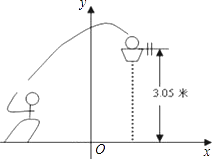
(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com