
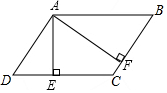
 如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.
如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$. 分析 根据AE⊥CD、AF⊥BC及∠EAF=60°可得∠C=120°,由平行四边形得出∠B=∠D=60°、AB∥CD且AB=CD,利用三角函数求得DE=2、AB=6,CE=4,最后可得$\overrightarrow{CE}$=$\frac{2}{3}$$\overrightarrow{CD}$=-$\frac{2}{3}$$\overrightarrow{DC}$=-$\frac{2}{3}$$\overrightarrow{AB}$.
解答 解:∵AE⊥CD、AF⊥BC,
∴∠AEC=∠AFC=90°,
∵∠EAF=60°,
∴∠C=360°-∠AEC-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
∴DE=ADcosD=4×$\frac{1}{2}$=2,AB=$\frac{BF}{cosB}$=$\frac{3}{\frac{1}{2}}$=6,
则CE=CD-DE=AB-DE=6-2=4,
∵AB∥CD,且AB=CD,
∴$\overrightarrow{CE}$=$\frac{2}{3}$$\overrightarrow{CD}$=-$\frac{2}{3}$$\overrightarrow{DC}$=-$\frac{2}{3}$$\overrightarrow{AB}$=-$\frac{2}{3}$$\overrightarrow{a}$,
故答案为:-$\frac{2}{3}$.
点评 本题主要考查四边形内角和、平行四边形的性质、三角函数的应用及平面向量的计算,熟练掌握平行四边形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
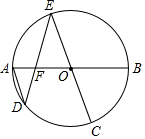 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在?ABCD中,点E,F分别在边BC和AD上,且CE=AF,
如图所示,在?ABCD中,点E,F分别在边BC和AD上,且CE=AF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.
本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
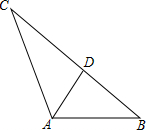 从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com