
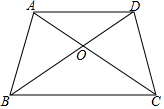
 已知梯形ABCD如图,AD∥BC,△AOD的面积是25,△DOC的面积是35,则梯形ABCD的面积是144.
已知梯形ABCD如图,AD∥BC,△AOD的面积是25,△DOC的面积是35,则梯形ABCD的面积是144. 分析 由△AOD的面积是25,△DOC的面积是35,根据等高三角形的面积比等于对应底的比,求得OA:OC的值,又由AD∥BC,可证得△AOD∽△COB,然后由相似三角形面积比等于相似比的平方,求得△BOC的面积,继而求得答案.
解答 解:∵△AOD的面积是25,△DOC的面积是35,
∴OA:OC=25:35=5:7,
∵AD∥BC,
∴△AOD∽△COB,
∴S△AOD:S△COB=($\frac{AO}{CO}$)2=$\frac{25}{49}$,
∴S△COB=25÷$\frac{25}{49}$=49,
∵S△ABC=S△DBC,
∴S△AOB=S△COD=35,
∴S梯形ABCD=25+35+49+35=144.
故答案为:144.
点评 此题考查了相似三角形的判定与性质以及梯形的性质.注意相似三角形的面积比等于相似比的平方、等高三角形面积的比等于其对应底的比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -(-3)和3 | B. | +(-5)和-[-(-5)] | C. | $\frac{1}{3}$和-3 | D. | -(-7)和-|-7| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -9没有平方根 | B. | ±1是1的平方根 | ||
| C. | -$\frac{1}{64}$的立方根为-$\frac{1}{4}$ | D. | 2的平方根为$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com