
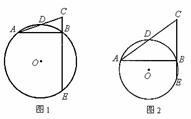
已知:在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E(如图1)。
在满足上述条件的情况下,当∠CAB的大小变化时,图形也随着改变(如图2),在这个变化过程中,有些线段总保持着相等的关系。
(1)观察上述图形,连结图2中已标明字母的某两点,得到一条新线段,证明它与线段CE相等;
(2)在图2中,过点E作⊙O的切线,交AC的延长线于点F。
①若CF=CD,求sin∠CAB的值;
②若![]() ,试用含n的代数式表示sin∠CAB(直接写出结果)。
,试用含n的代数式表示sin∠CAB(直接写出结果)。
(1)连结__________________
求证:_________=CE
证明:
(2)解:①
②![]() _____________(
_____________(![]() )
)
(1)证法一:如图3,连结OD
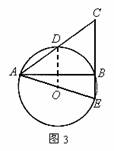
∵∠ABC=90°,CB的延长线交⊙O于点E
∴∠ABE=90° ∴AE是⊙O的直径
∵D是AC的中点,O是AE的中点
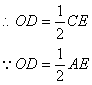 ∴AE=CE
∴AE=CE
证法二:如图4,连结BD
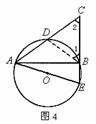
在Rt△ABC中,∠ABC=90°
∵D是AC的中点
∴AD=CD=BD ∴∠1=∠2
∵四边形AEBD内接于⊙O
∴∠1=∠DAE ∴∠2=∠DAE ∴AE=CE
证法三:如图5,连结DE

同证法一,得AE是⊙O的直径 ∴∠ADE=90°
∵D是AC的中点
∴DE是线段AC的垂直平分线
∴AE=CE
(2)①解法一:根据题意画出图形,如图6,连结DE。
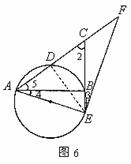
∵EF是⊙O的切线
∴∠3=∠4,且![]()
![]()
设![]() ,则
,则![]()
![]()
∵AE是⊙O的直径 ∴∠AEF=90°
在Rt△AEF中,![]()
![]()
![]()
解法二:根据题意画出图形,如图7,连结DE。
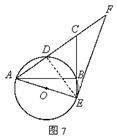
∵AE是⊙O的直径,EF是⊙O的切线
∴∠ADE=∠AEF=90°
∴Rt△ADE∽Rt△EDF
![]()
设![]() ,则
,则![]()
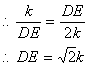
在Rt△CDE中
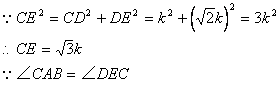
![]()
②![]() (
(![]() )
)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
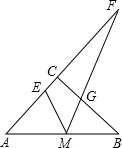 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
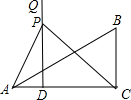 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com