
分析 根据题意,分3种情况:①当x1≤x2≤-$\frac{3}{2}$时;②当x1≤-$\frac{3}{2}$≤x2时;③当-$\frac{3}{2}$<x1≤x2时;然后根据二次函数的最值的求法,求出满足题意的实数x1、x2(x1<x2),使得当x1≤x≤x2时,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$即可.
解答 解:①当x1≤x2≤-$\frac{3}{2}$时,二次函数y=x2+3x-4单调递减,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}+3{x}_{1}-4=\frac{12}{{x}_{1}}}\\{{{x}_{2}}^{2}+3{x}_{2}-4=\frac{12}{{x}_{2}}}\end{array}\right.$,
由x${{\;}_{1}}^{2}$+3x1-4=$\frac{12}{{x}_{1}}$,
解得x1=-3,-2,2,
由x${{\;}_{2}}^{2}$+3x2-4=$\frac{12}{{x}_{2}}$,
解得x2=-3,-2,2,
∵x1≤x2≤-$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{x}_{2}=-2}\end{array}\right.$
②当x1≤-$\frac{3}{2}$≤x2时,
Ⅰ、当-$\frac{3}{2}$-x1≥x2-(-$\frac{3}{2}$)时,
可得x1+x2≤-3,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{\frac{4×1×(-4)-{3}^{2}}{4×1}=\frac{12}{{x}_{2}}①}\\{{{x}_{1}}^{2}+3{x}_{1}-4=\frac{12}{{x}_{1}}②}\end{array}\right.$,
由①,可得x2=-$\frac{48}{25}$,
由(2),可得x1=-3,-2,2,
∵x1≤-$\frac{3}{2}$<x2,-$\frac{3}{2}$>-$\frac{48}{25}$,
∴没有满足题意的x1、x2.
Ⅱ、当-$\frac{3}{2}$-x1<x2-(-$\frac{3}{2}$)时,
可得x1+x2>-3,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{\frac{4×4×(-4)-{3}^{2}}{4×1}=\frac{12}{{x}_{2}}}\\{{{x}_{2}}^{2}+3{x}_{2}-4=\frac{12}{{x}_{1}}}\end{array}\right.$
解得$\left\{\begin{array}{l}{{x}_{1}=-\frac{1875}{949}}\\{{x}_{2}=-\frac{48}{25}}\end{array}\right.$
∵x1+x2=-$\frac{1875}{949}$≈-1.98-1.92=-3.9<-3,
∴没有满足题意的x1、x2.
③当-$\frac{3}{2}$<x1≤x2时,
二次函数y=x2+3x-4单调递增,
∵y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}+3{x}_{1}-4=\frac{12}{{x}_{2}}①}\\{{{x}_{2}}^{2}+3{x}_{2}-4=\frac{12}{{x}_{1}}②}\end{array}\right.$,
(1)×x2-(2)×x1,可得
(x1-x2)(x1x2+4)=0,
∵x1-x2≠0,
∴x1x2+4=0,
∴x2=-$\frac{4}{{x}_{1}}$…(1),
把(3)代入(1),可得x1=-3±$\sqrt{13}$,
∵x1>-$\frac{3}{2}$,
∴x1=$\sqrt{13}$,
∴x2=$\frac{-4}{{x}_{1}}$,
∵-$\sqrt{13}$-3<-$\frac{3}{2}$,
∴没有满足题意的x1、x2.
综上,可得
x1=-3,x2=-2时,当x1≤x≤x2时,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.
∴x1+x2=-5,
故答案为:-5.
点评 此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力,此题还考查了待定系数法求二次函数的解析式的方法,以及二次函数的最值的求法,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
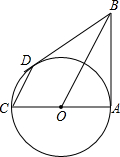 如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.
如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com