
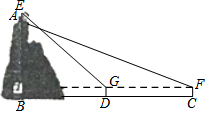
 某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下:
某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下:分析 设AB=x,用x的代数式表示AH、FH,在Rt△AHF中,根据tan∠AFH=$\frac{AH}{HF}$,列出方程即可解决问题.
解答 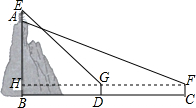 解:设AB=x,由题意BH=DG=CF=1.6米,FG=CD=400米.
解:设AB=x,由题意BH=DG=CF=1.6米,FG=CD=400米.
∴AH=(x-1.6)米,
∵∠EGH=45°,∠EHG=90°,
∴∠E=∠HGE=45°,
∴HE=HG=(x-1.6+10)米.
在Rt△AHF中,tan∠AFH=$\frac{AH}{HF}$,
∴tan22°=$\frac{x-1.6}{x-1.6+10+400}$,
∴0.4═$\frac{x-1.6}{x-1.6+10+400}$,
解得x≈275.
∴山峰与中心广场的相对高度AB约为275米.
点评 本题考查解直角三角形-仰角俯角问题,解题的关键是学会设未知数,利用三角函数构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 纸环数x(个) | 1 | 2 | 3 | 4 | … |
| 彩纸链长度y( cm) | 19 | 36 | 53 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.
如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com