
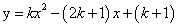 已知二次函数 (
已知二次函数 (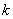 ¹0为实数))。
¹0为实数))。
(1) 求证:不论k为何值,该函数的图像与x轴总有两个公共点;
(2) 该函数的图像与x轴交于A、B两点,与y轴交于点C。
当△ABC的面积等于2时,求k的值:
‚对任意负实数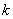 ,当x>m时,
,当x>m时,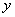 随着
随着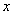 的增大而减小,试求出
的增大而减小,试求出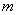 的一个值
的一个值
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
|
| A. | (0,2) | B. | (0,3) | C. | (0,4) | D. | (0,7) |
查看答案和解析>>
科目:初中数学 来源: 题型:
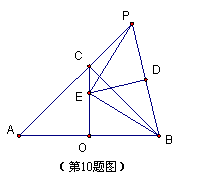
如图,AB为等腰直角⊿ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )
①E为⊿ABP的外心;②∠PEB=90°;
③PC·BE = OE·PB; ④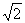 CE + PC=
CE + PC=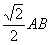 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,函数y1=|x|和y2=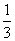 x+
x+ 的图象相交于(-1,1) (2,2)两点.当y1 <y2时,x的取值范围是( )
的图象相交于(-1,1) (2,2)两点.当y1 <y2时,x的取值范围是( )
A.x<-1 B.-1<x<2 C.x>2 D.x<-1或x>2

查看答案和解析>>
科目:初中数学 来源: 题型:
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.求证:△ABM与△ABN的面积相等.
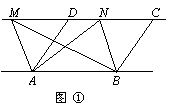

②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.


(2)结论应用:
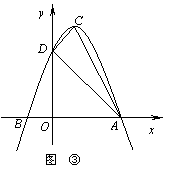
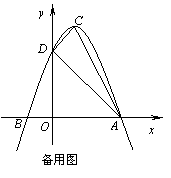
如图③,抛物线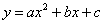 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线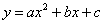 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.【改编】
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.【改编】


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com