
【题目】在△ABC中,AB=AC,∠BAC=110°,MP、NO分别垂直平分AB、AC.则∠PAO=___________;

科目:初中数学 来源: 题型:
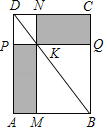
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() ∥
∥![]() 轴,
轴, ![]() .
.

⑴.求点![]() 的坐标:
的坐标:
⑵.四边形![]() 的面积
的面积![]() 四边形
四边形![]() ;
;
⑶. 在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() ;若存在,求出点
;若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种广场三联漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF

(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出D点的坐标.
(2)连接OB,OD,BD,请求出三角形OBD的面积.
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,当边BC与x轴重合时,停止运动,设运动的时间为t秒,t为多少时,三角形OBD的面积等于长方形ABCD的面积的![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com