
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P��a��b���͵�Q��a��b'�����������¶��壺
��b'=![]() ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
��1���ٵ㣨��![]() ��1�����ޱ����������� ����
��1�����ޱ����������� ����
���ڵ�A����1��2����B����2����1������һ�����Ǻ���y=![]() ͼ����ijһ��������㣬��������� ����
ͼ����ijһ��������㣬��������� ����
��2������P�ں���y=��x+3��ͼ���ϣ�����2��x��6ʱ�������ޱ��Q��������b'��ȡֵ��Χ��
��3������P�ڹ���x�Ķ��κ���y=x2��2tx+t2+t��ͼ���ϣ����ޱ��Q��������b'��ȡֵ��Χ��b'��m��b'��n������m��n����s=m��n����s����t�ĺ�������ʽ��s��ȡֵ��Χ��
���𰸡���1��������![]() ����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
��������
��1����ֱ�Ӹ����ޱ��Ķ���ֱ�ӵó��𰸣�
�ڵ㣨-1��-2���ڷ���������ͼ���ϣ��㣨-1��-2�����ޱ��Ϊ��-1��2�����ݴ˵õ��𰸣�
��2�����������֪y=-x+3��x��-2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ����ͼ�ɵõ��𰸣�
��ͼ���ϣ����ͼ�ɵõ��𰸣�
��3���������y=x2-2tx+t2+t�������꣬���t��1�Ĺ�ϵȷ��y����ֵ��������m��n��ʾ��s������t��ȡֵ��Χ���s��ȡֵ��Χ��
��1���ٸ����ޱ��Ķ����֪��㣨��![]() ��1�����ޱ�������Ϊ����
��1�����ޱ�������Ϊ����![]() ����1����
����1����
������1����2���ޱ��Ϊ����1��2������������ǵ�A��
��2�������⣬y=��x+3��x�ݩ�2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��x=��2ʱ��y=��2��3=��5��
��x=1ʱ��y=��1+3=2��
��x=6ʱ��y=��6+3=��3��
�൱��2��x��6ʱ����5��b���2��
��3����y=x2��2tx+t2+t=��x��t��2+t��
�ඥ������Ϊ��t��t����
��t��1��b����ȡֵ��Χ��b���m��b�䣼n�������ⲻ����
��t��1����x��1ʱ��y����СֵΪt����m=t��
��x��1ʱ��y��ֵС�ک�[��1��t��2+t]����n=��[��1��t��2+t]��
��s=m��n=t+��1��t��2+t=t2+1��
��s����t�ĺ�������ʽΪs=t2+1��t��1����
��t=1ʱ��sȡ��Сֵ2��
��s��ȡֵ��Χ��s��2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ������������
������������![]() �ἰ���Ϸ��IJ��ּ���
�ἰ���Ϸ��IJ��ּ���![]() ����
����![]() ����ƽ�Ƶ�
����ƽ�Ƶ�![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����ֱ��
����ֱ��![]() ��
��![]() ��
��![]() ����
����![]() ����ͬ�Ľ��㣬��
����ͬ�Ľ��㣬��![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ��Ķ����ڵ�һ���ޣ��ҹ��㣨0��1���ͣ���1��0�������н��ۣ���ab��0����b2��4����0��a+b+c��2����0��b��1���ݵ�x����1ʱ��y��0��������ȷ���۵ĸ����ǣ�������
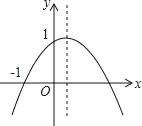
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ĵ�����װ��2�������1��������Щ�����ɫ�ⶼ��ͬ�����Ⱥ������������1�����Żأ����ٴ����µ�2��������������1����
��1������״ͼ���б��ȷ����г����п��ܳ��ֵĽ����
��2�������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON��30������A1��A2��A3��������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ��������1���ȱ������εı߳���a1����2���ȱ������εı߳���Ϊa2���Դ����ƣ���OA1��3����a2=_______��a2019=_______.
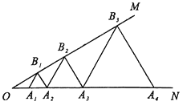
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��A(2,4),B(4,2),��x����ȡһ��P,ʹ��P����A�͵�B�ľ���֮����С,���P��������_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90����OA=90cm��OB=30cm��һ�������ڵ�B������һ��С��ӵ�A��������AO�������ٹ����O�������������ӵ�B��������ֱ������ǰ������С����ǡ���ڵ�C����ס��С�������С��������ٶ�����������ߵ��ٶ��������ô���������ߵ�·��BC�Ƕ���?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
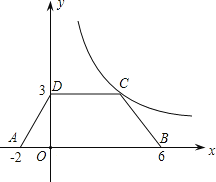
����Ŀ����ͼ����������ABCD������ƽ������ϵ�У���֪A����2��0����B��6��0����D��0��3����������������ͼ����C��
��1�����C������ͷ����������Ľ���ʽ��
��2������������ABCD����ƽ��2����λ���ʵ�B�Ƿ�����˫�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB=AC=AD��AD��BC��
(1)��֤��BDƽ�֡�ABC��
(2)����C=78�������D�Ķ���.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com