
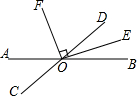
 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,EO⊥FO于O,若∠BOE=20°.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,EO⊥FO于O,若∠BOE=20°.分析 (1)根据角平分线的性质可得∠DOE=∠BOE=$\frac{1}{2}$∠BOD,再由∠BOE=20°可得∠BOD的度数,然后再根据对顶角相等可得答案;
(2)根据垂直定义可得∠EOF=90°,再利用平角定义计算出∠AOF的度数,然后可得∠COF的度数.
解答 解:(1)∵OE是∠BOD的平分线,
∴∠DOE=∠BOE=$\frac{1}{2}$∠BOD,
∵∠BOE=20°,
∴∠BOD=40°,
∴∠AOC=40°;
(2)∵EO⊥FO于O,
∴∠EOF=90°,
∵∠BOE=20°,
∴∠AOF=180°-90°-20°=70°,
∴∠COF=70°+40°=110°.
点评 此题主要考查了垂直定义、角平分线定义和对顶角性质,关键是理清图中角之间的关系.


科目:初中数学 来源: 题型:填空题
 如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.
如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
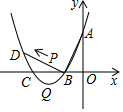 如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.
如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
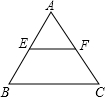 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )| A. | 15米 | B. | 20米 | C. | 25米 | D. | 30米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com