
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
分析 (1)根据计划投入资金不多于35万元,且获利多于15万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数;
(2)得出利润y与A产品数量x的函数关系式,根据增减性可得,B产品生产越多,获利越大,因而B取最大值时,获利最大,据此即可求解.
解答 解:(1)设生产A种产品x件,则B种产品(10-x)件,由题意得
$\left\{\begin{array}{l}2x+5(10-x)≤35\\ x+3(10-x)>15\end{array}$
解得5≤x<7.5,
因为x为整数,所以x=5,6,7,
所以,工厂有3种生产方案:
方案①,A种产品5件,则B种产品5件;
方案②,A种产品6件,则B种产品4件;
方案③,A种产品7件,则B种产品3件,
(2)设A种产品x件时,获得的利润为W万元,则
W=x+3(10-x)=-2x+30,
因为-2<0,所以W随x的增大而减小,
所以,当x=5时,W取得最大值为20,
所以,生产方案①获利最大,最大利润为20万元.
点评 本题考查理解题意的能力,关键从表格种获得成本价和利润,然后根据利润这个等量关系列方程,根据第二问中的利润和成本做为不等量关系列不等式组分别求出解,然后求出哪种方案获利最大从而求出来.


科目:初中数学 来源: 题型:解答题
 已知△ABC.
已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
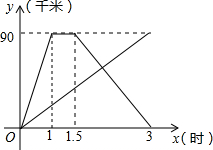 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-3,-2) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
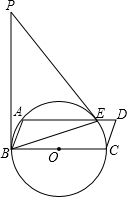 如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.
如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com