
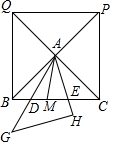
 如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.
如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.分析 (1)只要证明∠DAM+∠EAM=∠BAD+∠EAC,由AD平分∠BAM,可得∠BAD=∠DAM即可推出∠EAM=∠EAC.
解答 (1)证明:∵∠DAE=45°,
∴∠DAM+∠EAM=45°,
在正方形BCPQ中,BP⊥CQ,∴∠BAC=90°,
∴∠BAD+∠CAE=45°,
∴∠DAM+∠EAM=∠BAD+∠EAC
AD平分∠BAM,
∴∠BAD=∠DAM
∴∠EAM=∠EAC 即AE平分∠MAC.
(2)解:结论:BD2+CE2=DE2.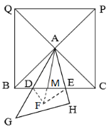
证明:延长AM到点F,使AF=AB,
在正方形BCPQ中,AB=AC,∠BAC=90°,
∴AF=AC,∠ABC=∠ACB=45°,
∵∠BAD=∠DAM 由(1)知,∠EAM=∠EAC,
又AF=AF,
∴△FAD≌△BAD,△FAE≌△CAE,
∴∠AFD=∠ABC=45°,DF=BD,∠AFE=∠ACB=45°,EF=EC,
∴∠DFE=90°,
在Rt△DEF中,DF2+EF2=DE2,
∴BD2+CE2=DE2.
点评 本题考查正方形的性质、角平分线的定义、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
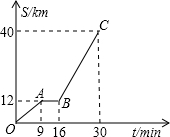 如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
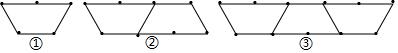
| 图形标号 | ① | ② | ③ | ④ | ⑤ | … | n | … |
| 火柴棒数 | 5 | 9 | 13 | 17 | 21 | … | 4n+1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象位于第一、三象限 | B. | 图象必经过点(-2,-3) | ||
| C. | y随x的增大而增大 | D. | 若x>2,则y<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
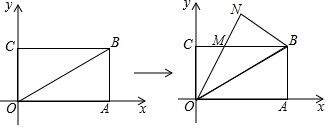
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图
尺规作图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com