
【题目】如图,点A(a,b)是抛物线![]() 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:过点A、B分别作x轴的垂线,通过构建相似三角形以及函数解析式来判断①②是否正确.![]() 的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
详解:过A.B分别作AC⊥x轴于C.BD⊥x轴于D,则:AC=b,OC=a,OD=c,BD=d;

(1)由于OA⊥OB,易知△OAC∽△BOD,有:
![]() 即
即![]()
∴ac=bd(结论②正确).
(2)将点A.B的坐标代入抛物线的解析式中,有:
![]() …Ⅰ、
…Ⅰ、![]() …Ⅱ;
…Ⅱ;
Ⅰ×Ⅱ,得:![]() 即
即![]() (结论①正确).
(结论①正确).
(3)![]() ,
,
![]() ,
,
![]()
由此可看出,△AOB的面积不为定值(结论③错误).
(4)设直线AB的解析式为:y=kx+h,代入A.B的坐标,得:
ak+h=b…Ⅲ、ck+h=d…Ⅳ
Ⅲ×cⅣ×a,得:![]()
∴直线AB与y轴的交点为(0,2)(结论④正确).
综上,共有三个结论是正确的,它们是①②④,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.

(1)求证:AP=AO;
(2)求证:PE⊥AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD与点E,连CD分别交AE、AB于点F、G,过点A作AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③△ADF≌△BAH;④ DF=2EH,其中正确结论的个数为( )
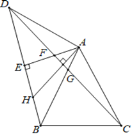
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两块完全相同的含30°的直角三角板叠放在一起,且∠DAB=30°,有以下四个结论,①AF⊥BC;②∠BOE=135°;③O为BC中点;④AG:DE=1:3,其中正确结论的序号是( )
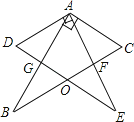
A.①②B.②④C.②③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com