
分析 (1)根据一元二次方程x2-2(a+1)x+a2+3=0的两实数根得到△=4(a+1)2-4(a+3)2=8a-8≥0,求出a的取值范围,结合(x1-1)(x2-1)=10,利用根与系数的关系即可求出a的值;
(2)分6是等腰三角形的腰长还是底边长,利用等腰三角形的性质求出a的值,进而求出等腰三角形的腰长或底边长,求出三角形的周长.
解答 解:(1)∵x1,x2是关于x的一元二次方程x2-2(a+1)x+a2+3=0的两实数根,
∴△≥0,即△=4(a+1)2-4(a+3)2=8a-8≥0,
∴a≥1,x1+x2=2(a+1),x1•x2=a2+3,
∵(x1-1)(x2-1)=10,
∴x1x2-(x1+x2)+1=10,a2+3-2(a+1)+1=10,
∴解得a1=4,a2=-2,
∵a≥1,
∴a=4;
(2)由题意可知,若等腰三角形的底边为6,那么方程x2-2(a+1)x+a2+3=0的两个根相等,
∴△=0,即△=4(a+1)2-4(a+3)2=8a-8=0,
∴a=1,
∴方程为x2-4x+4=0,解得x1=x2=2,
∵2+2<6不能构成三角形,故舍去,
若等腰三角形的腰长为6,那么方程x2-2(a+1)x+a2+3=0的一个根为6,
∴把6代入方程求得36-12(a+1)+a2+3=0,解得a的值为3或9,
当a=3时,方程x2-8x+12=0,解得x1=2,x2=6,
∴此三角形的周长为6+6+2=14,
当a=9时,方程为x2-20x+84=0,解得x1=14,x2=6,
∵6+6<14构不成三角形,故舍去,
∴综上可知三角形的周长为14.
点评 本题主要考查了根与系数的关系、跟的判别式、三角形三边关系以及等腰三角形的性质,解答本题的关键是要熟练掌握等腰三角形的性质,注意分类讨论,此题难度一般.


科目:初中数学 来源: 题型:解答题
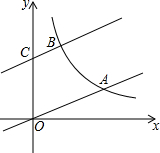 如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.
如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
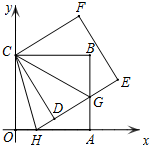 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
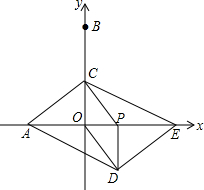 如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造平行四边形PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.
如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造平行四边形PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 27π | B. | $\frac{27}{4}$π | C. | 9π | D. | $\frac{9}{4}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 64的立方根是±$\root{3}{64}$=±$\sqrt{4}$ | B. | -$\frac{1}{2}$是-$\frac{1}{6}$的立方根 | ||
| C. | $\root{3}{-27}$=-$\root{3}{27}$ | D. | 立方根等于它本身的数是0和1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com