练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．分式$\frac{1}{3{x}^{2}{y}^{2}}$，-$\frac{1}{4x{y}^{3}}$的最简公分母是12x2y3．

    分析 各系数的最小公倍数，则系数为12，相同字母的最高次幂，则为x2y3，结果为：12x2y3．

    解答 解：分式$\frac{1}{3{x}^{2}{y}^{2}}$，-$\frac{1}{4x{y}^{3}}$的最简公分母是：12x2y3，
    故答案为：12x2y3．

    点评 本题考查了最简公分母，熟练掌握最简公分母的求法是关键：就是各系数的最小公倍数，相同字母的最高次幂，所有不同字母都写在积里．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．观察下列各式的特点：
    $\sqrt{1}$=1，$\sqrt{1+3}$=2，$\sqrt{1+3+5}$=3，$\sqrt{1+3+5+7}$=4，…
    计算：$\frac{1}{\sqrt{1}×\sqrt{1+3}}$+$\frac{1}{\sqrt{1+3}×\sqrt{1+3+5}}$+…+$\frac{1}{\sqrt{1+3+…+2015}×\sqrt{1+3+…+2017}}$=$\frac{1008}{1009}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，直线AB、CD相交于点O，OE平分∠AOC，∠BOC-∠BOD=30°，则∠COE的度数是37.5°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．把下列各式的分母有理化．
    $\frac{\sqrt{10}}{\sqrt{5}}$=$\sqrt{2}$；$\frac{\sqrt{6}}{\sqrt{24}}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

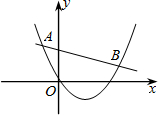    8．已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象交于点A（-2，4），B（5，1），如图所示，则能使y1＞y2成立的x的取值范围是x＜-2或x＞5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知x=$\sqrt{\frac{a-\sqrt{{a}^{2}-4}}{2a}}$（a＞0），那么$\frac{x}{\sqrt{1-{x}^{2}}}$+$\frac{\sqrt{1-{x}^{2}}}{x}$=a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．用直接开平方法解方程．
    （1）x2-$\frac{36}{25}$=0
    （2）3x2-9=0
    （3）（x-2）2=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，有两条公路OM，ON相交成30°角．沿公路OM方向离O点80米处有一所学校A，当重型运输卡车P沿道路ON方向行驶时，在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时．
    （1）求对学校A的噪声影响最大时卡车P与学校A的距离；
    （2）求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

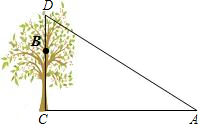    11．如图，一棵树CD，在其6m高的点B处有两只猴子，它们都要到A处池塘边喝水，其中一只猴子沿树爬下走到离树12m处的池塘A处，另一只猴子爬到树顶D后直线跃向池塘的A处．如果两只猴子所经过的路程相等，试问这棵树有多高？

    查看答案和解析>>

    同步练习册答案