
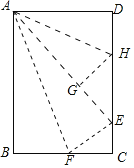
【题目】在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF,点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上,若AD=6,CD=10,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
利用翻折不变性可得AE=AB=10,推出DE=8,EC=2,设BF=EF=x,在Rt△EFC中,x2=22+(6-x)2,可得x=![]() ,设DH=GH=y,在Rt△EGH中,y2+42=(8-y)2,可得y=3,由此即可解决问题.
,设DH=GH=y,在Rt△EGH中,y2+42=(8-y)2,可得y=3,由此即可解决问题.
∵四边形ABCD是矩形,
∴∠C=∠D=90°,AB=CD=10,AD=BC=6,
由翻折不变性可知:AB=AE=10,AD=AG=6,BF=EF,DH=HG,
∴EG=4,
在Rt△ADER中,DE=![]() =8,
=8,
∴EC=10﹣8=2,
设BF=EF=x,在Rt△EFC中有:x2=22+(6﹣x)2,
∴x=![]() ,
,
设DH=GH=y,在Rt△EGH中,y2+42=(8﹣y)2,
∴y=3,
∴EH=5,
∴ ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
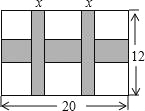
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
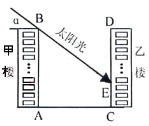
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次涵数![]() 的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数
的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数![]() 的图象.
的图象.
(1)试确定![]() ,
,![]() ,
,![]() 的值;
的值;
(2)指出二次函数![]() 图象的开口方向、对称轴和顶点坐标.
图象的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
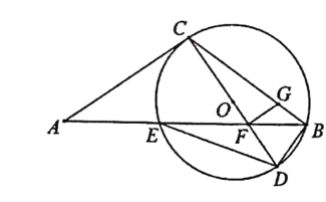
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
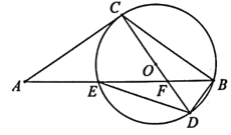
(1)求⊙O的直径.
(2)过点F作FG⊥CD交BC于点G,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A. “任意选择某一电视频道,它正在播放动画片”是必然事件
B. 某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,一定有4次投中
C. 任意抛掷一枚均匀的硬币,反面朝上的概率为![]()
D. 布袋里有3个白球,1个黑球.任意取出1个球,恰好是黑球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
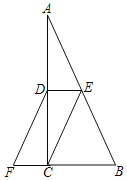
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸(![]() ),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生产标准,产品等级规定如下:
尺寸(单位: | 产品等次 |
| 特等品 |
| 优等品 |
| 合格品 |
| 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格个数时,将优等品(含特等品)算在内,
(1)已知此次抽检的合格率为![]() ,请判断编号为15的产品是否为合格品,并说明理由;
,请判断编号为15的产品是否为合格品,并说明理由;
(2)已知此次及抽检出的优等品尺寸的中位数为![]() .
.
①![]() __________;
__________;
②将这些优等品分成两组,一组尺寸大于![]() ,另一种尺寸不大于
,另一种尺寸不大于![]() ,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com