
分析 (1)根据所给等式发现$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
(2)根据$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$,可得(2)的计算过程及结果.
解答 解:(1)∵$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
故答案为:$\frac{1}{n}-\frac{1}{n+1}$;
(2)$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$=$\frac{1}{2}×$($\frac{1}{2}-\frac{1}{4}$)+$\frac{1}{2}$×($\frac{1}{4}-\frac{1}{6}$)$+\frac{1}{2}$×($\frac{1}{6}$$-\frac{1}{8}$)+…+$\frac{1}{2}$×($\frac{1}{2014}-\frac{1}{2016}$)
=$\frac{1}{2}×$($\frac{1}{2}-\frac{1}{4}$$+\frac{1}{4}-\frac{1}{6}$$+\frac{1}{6}-\frac{1}{8}$+…+$\frac{1}{2014}-\frac{1}{2016}$)
=$\frac{1}{2}$×($\frac{1}{2}-\frac{1}{2016}$)
=$\frac{1}{2}×$$\frac{1007}{2016}$
=$\frac{1007}{4032}$.
点评 本题主要考查了数字的变化规律,发现规律,运用规律是解答此题的关键.


科目:初中数学 来源: 题型:选择题
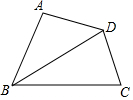 如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )| A. | 10 | B. | 12 | C. | 20 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.
如图,四边形ABCD中,BD与AC相交于E点,AE=CE,BC=AC=DC,则tan∠ABD•tan∠ADB=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
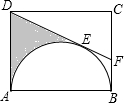 矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.
矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
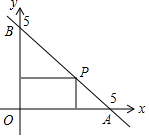 如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )
如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )| A. | 5 | B. | 7.5 | C. | 10 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com