
分析 根据平均数定义有$\frac{1}{3}$(x-18+y+13+z-25)=12求得x+y+z的值,由x,y,z为连续的偶数且x<y<z,设x=2k,则y=2k+2,z=2k+4,代入x+y+z=66求得k的值,即可知x、y、z,代入原数据可得答案.
解答 解:根据题意知,$\frac{1}{3}$(x-18+y+13+z-25)=12,
得:x+y+z=66,
∵x,y,z为连续的偶数且x<y<z,
∴设x=2k,则y=2k+2,z=2k+4,
∴2k+2k+2+2k+4=66,
解得:k=10,
故x=20,y=22,z=24,
∴这组数据的三个数分别是2,35,-1.
点评 此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:对于n个数x1,x2,…,xn,则$\overline{x}$=$\frac{1}{n}$(x1+x2+…+xn)就叫做这n个数的算术平均数.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
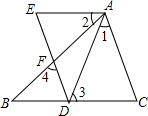 完成证明,说明理由.
完成证明,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
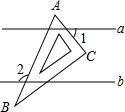 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
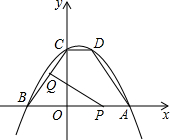 如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.
如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
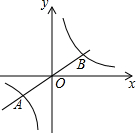 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com