
分析 分两种情况探讨:点A落在矩形对角线BD上,点A落在矩形对角线AC上,在直角三角形中利用勾股定理列出方程,通过解方程可得答案.
解答 解:①点A落在矩形对角线BD上,如图1所示.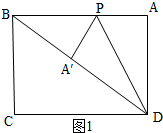
∵AB=16,AD=12,
∴BD=20,
根据折叠的性质,AD=A′D=12,AP=A′P,∠A=∠PA′D=90°,
∴BA′=8,
设AP=x,则BP=16-x,
∵BP2=BA′2+PA′2,
∴(16-x)2=x2+82,
解得:x=6,
∴AP=6;
②点A落在矩形对角线AC上,如图2所示: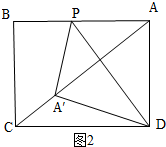
由折叠的性质可知PD垂直平分AA′,
∴∠BAC+∠A′AD=∠PDA+∠A′AD=90°.
∴∠BAC=∠PDA.
∴tan∠BAC=tan∠PDA.
∴$\frac{BC}{AB}=\frac{AP}{AD}$即$\frac{12}{16}$=$\frac{AP}{12}$.
∴AP=9.
综上所述AP的长为6或9.
故答案为:6或9.
点评 本题考查了折叠问题、勾股定理,矩形的性质以及三角形相似的判定与性质;依据翻折的性质找准相等的量是解题的关键.


科目:初中数学 来源: 题型:填空题
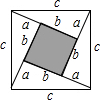 如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
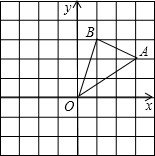 如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
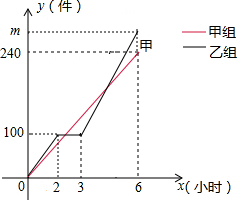 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )| A. | 甲组加工零件数量y与时间x的关系式为y甲=40x | |
| B. | 乙组加工零件总量m=280 | |
| C. | 经过2$\frac{1}{2}$小时恰好装满第1箱 | |
| D. | 经过4$\frac{3}{4}$小时恰好装满第2箱 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.
如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com