练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图，已知AB∥CD，∠BAE=3∠ECF，∠ECF=28°，求∠E的度数．

    分析 由∠ABE=3∠ECF，∠ECF=28°，即可求得∠ABE的度数，又由AB∥CD，根据两直线平行，同位角相等，即可求得∠DFE的度数，又由三角形外角的性质，即可求得∠E的度数．

    解答 解：∵∠ABE=3∠ECF，∠ECF=28°，
    ∴∠ABE=84°，
    ∵AB∥CD，
    ∴∠DFE=∠ABE=84°，
    ∵∠DFE=∠ECF+∠E，
    ∴∠E=∠DFE-∠ECF=84°-28°=56°．

    点评 此题考查了平行线的性质．此题比较简单，解题的关键是注意两直线平行，同位角相等定理的应用，注意数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知抛物线y=ax2，点P、Q为抛物线对称轴上两点，且P、Q关于抛物线顶点对称，过Q点任意作一条直线与抛物线交于A、B两点，求证：抛物线对称轴平分∠APB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

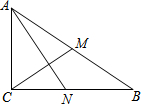    19．如图，Rt△ABC中，∠ACB=90°，CM为AB边上的中线，AN⊥CM，交BC于点N．若CM=3，AN=4，则tan∠CAN的值为$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．因式分解：$\frac{1}{3}{a}^{3}$-3a=$\frac{1}{3}$a（a+3）（a-3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

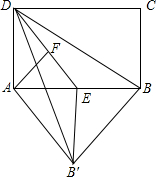    3．在矩形ABCD中，E为AB边上的中点，将△BDE翻折，B的对应点记为B′，已知AD=4，AB=6，F为线段DE上一动点，当∠DAF=∠BAB′时，则DF+BB′=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：
    （$\frac{1}{x-y}$-$\frac{1}{{x}^{2}-xy}$）÷$\frac{x-2}{3x}$，其中x=2+tan60°，y=4sin30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列命题为真命题的是（　　）
    A．平分弦的直径垂直于弦
    B．在同圆或等圆中、相等的弦所对的圆周角相等
    C．平分弦所对的一条弧的直径一定垂直平分这条弦
    D．相等的圆心角所对的弧相等，所对的弦也相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解下列不等式，并把解集在数轴上表示出来
    （1）3（x+2）-5x＜-3
    （2）1-$\frac{x-2}{3}$≥$\frac{x+1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知：8•2 2m-1•23m=217，求m的值．

    查看答案和解析>>

    同步练习册答案