
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
【答案】(1)甲公司单独完成这项任务需要9天,乙公司单独完成这项任务需要18天(2)甲公司至多工作4天
【解析】
(1)设甲公司单独完成这项任务需要x天,则乙公司单独完成这项任务需要2x天,根据甲公司完成的任务量+乙公司完成的任务量=总任务量,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设甲公司工作m天,则乙公司工作(18﹣2m)天,根据完成这项工作的总费用不超过40万元,即可得出关于m的一元一次不等式,解之取其最大值即可得出结论.
解:(1)设甲公司单独完成这项任务需要x天,则乙公司单独完成这项任务需要2x天,
依题意,得:![]() =1,
=1,
解得:x=9,
经检验,x=9是原方程的解,且符合题意,
∴2x=18.
答:甲公司单独完成这项任务需要9天,乙公司单独完成这项任务需要18天.
(2)设甲公司工作m天,则乙公司工作![]() =(18﹣2m)天,
=(18﹣2m)天,
依题意,得:5m+2(18﹣2m)≤40,
解得:m≤4.
答:甲公司至多工作4天.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)﹣(3)题
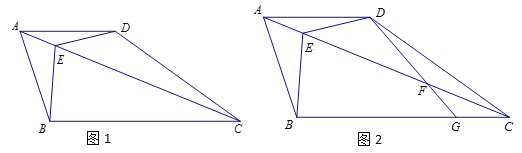
数学课上,老师出示了这样一道题:如图,四边形ABCD,AD∥BC,AB=AD,E为对角线AC上一点,∠BEC=∠BAD=2∠DEC,探究AB与BC的数量关系.
某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现∠ACB=∠ABE”;
小源:“通过观察和度量,AE和BE存在一定的数量关系”;
小亮:“通过构造三角形全等,再经过进一步推理,就可以得到线段AB与BC的数量关系”.
……
老师:“保留原题条件,如图2, AC上存在点F,使DF=CF=![]() AE,连接DF并延长交BC于点G,求
AE,连接DF并延长交BC于点G,求![]() 的值”.
的值”.
(1)求证:∠ACB=∠ABE;
(2)探究线段AB与BC的数量关系,并证明;
(3)若DF=CF=![]() AE,求
AE,求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校 | 平均分 | 中位数 | 众数 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种落地晾衣架如图①所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图②是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85 cm,BO=DO=65 cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为______cm.(参考数据:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①abc<0;②2a﹣b=0;③a+b+c<0;④4ac﹣b2<0;其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
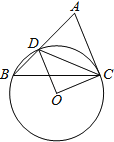
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与y轴交于点B,与抛物线
,与y轴交于点B,与抛物线![]() 的对称轴交于点
的对称轴交于点![]() .
.
(1)求m的值;
(2)求抛物线的顶点坐标;
(3)![]() 是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点
是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点![]() ,
,![]() (点P在点Q的左侧).若
(点P在点Q的左侧).若![]() 恒成立,结合函数的图象,求a的取值范围.
恒成立,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC内接于⊙O,AD⊥BC于点D,连接AO.
(1)如图1,求证:∠BAO=∠CAD;
(2)如图2,CE⊥AB于点E,交AD于点F,过点O作OH⊥BC于点H,求证:AF=2OH;
(3)如图3,在(2)的条件下,若AF=AO,tan∠BAO=![]() ,BC=
,BC=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
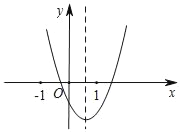
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com