
| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
分析 (1)根据表格中的数据可以求得a的值;
(2)根据表格中的数据可以得到优等品的概率;
(3)首先,根据概率的知识可以判断小明的说法是否正确,然后说明理由即可.
解答 解:(1)由题意可得,
a=450÷500=0.9,
故答案为:0.9;
(2)根据表格中的数据,可知从这批羽毛球中任取一个,为优等品的概率约为0.9,
故答案为:0.9;
(3)小明的说法不正确,
因为题目中表格的数据反映的是优等品出现的概率,也就是可能性大小,从这批羽毛球中抽取10个,可能都是优等品,也可能都不是优等品,故小明的说法错误.
点评 本题考查利用频率估计概率,解答本题的关键是明确概率的定义,利用概率的知识解答.


科目:初中数学 来源: 题型:解答题
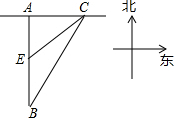 阅读材料,回答问题
阅读材料,回答问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
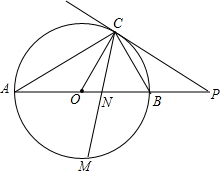 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-7=3y+1 | B. | 5x2-$\frac{1}{x}$-2=0 | C. | $\frac{1}{3}$x-5=$\frac{{x}^{2}}{2}$ | D. | ax2+bx+c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com