
【题目】四边形ABCD中,∠A=145°,∠D=75°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
【答案】(1)∠C=70°;(2)∠C=70°;(3)①∠BEC=110°;②不变.∠BEC=110°.
【解析】
(1)先根据四边形内角和等于360°求出∠B+∠C的度数,再除以2即可求解;
(2)先根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,再根据四边形内角和等于360°求出∠BEC的度数;
(3)①先根据四边形内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数;
②先根据三角形内角和等于180°求出∠FBC+∠BCF的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数.
(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°-∠A=180°-145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°-(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°-40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,M、N分别是AC、BD的中点,连接MN
(1)求证:MN⊥BD.
(2)若∠DAC=62°,∠BAC=58°,求∠DMB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,![]() ,
,![]() ,点P是对角线AC上的动点
,点P是对角线AC上的动点![]() 不与点A,C重合
不与点A,C重合![]() ,连接PD,作
,连接PD,作![]() 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.

![]() 线段PD的最小值为______;
线段PD的最小值为______;
![]() 求证:
求证:![]() ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值;
![]() 是否存在这样的点P,使得
是否存在这样的点P,使得![]() 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形ABCD中,AB=8cm,BC=12cm,E为AB的中点,动点P在线段BC上以4cm/s的速度由点B向C运动,同时,动点Q在线段CD上由点C向点D运动,设运动时间为t(s).

(1)当t=2时,求△EBP的面积;
(2)若动点Q以与动点P不同的速度运动,经过多少秒,△EBP与△CQP全等?此时点Q的速度是多少?
(3)若动点Q以(2)中的速度从点C出发,动点P以原来的速度从点B同时出发,都逆时针沿长方形ABCD的四边形运动,经过多少秒,点P与点Q第一次在长方形ABCD的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
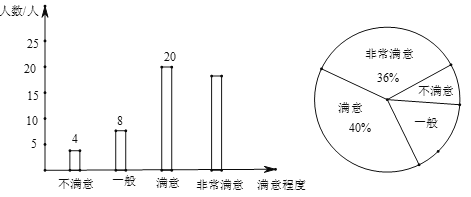
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为 人,其中“非常满意”的人数为 人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:
某校150名学生上学方式的分布表
方式 | 划记 | 人数 |
步行 | 正正正 | 15 |
骑车 | 正正正正正正 正正正正 | 51 |
乘公共交 通工具 | 正正正正正 正正正正 | 45 |
乘私家车 | 正正正正正正 | 30 |
其他 | 正 | 9 |
合计 | 150 |
(1)理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,那么这样的抽取是否合理?请说明理由.答:__________________________________.

(2)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地.请你结合上述统计的全过程,再提出一条合理化建议:________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com