Question

10．如图1，如果一条直线截一个三角形的任意两边，把这个三角形分成了一个四边形和一个三角形．若这个四边形的四个顶点在同一个圆上，则称这条直线为该三角形的一条共圆线．
（1）如图1，DE为△ABC的一条共圆线，判断△ABC被DE所分成的三角形与△ABC的形状有什么关系？并说明理由；
（2）如图2，在Rt△ABC中，∠C=90°，AB=5，AC=3，点P是边BC上的一点，PC=1，求过P的共圆线被△ABC两边截得的线段长；
（3）如图3，A（1，3），B（-3，0），C（4，0），点P为线段BC上一动点，设CP=x，若过P存在△ABC的共圆线，求x的取值范围．

Answer 1

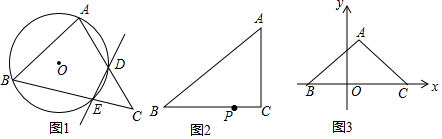
分析 （1）相似，根据四点共圆时，圆外角等于它的内对角得：∠EDC=∠B，利用两角对应相等，则两三角形相似；
（2）如图2，过P作PD⊥AB于D，根据对角互补的四边形四点共圆，可得A、D、P、C四点共圆，则直线PD就是△ABC的共圆线，分别求出AD、BD、BP、PC的长即可；
（3）分两种情况：第一种：如图4和图5，过P的直线与A、C共圆，根据∠ACD=45°，求出x的最小值为$\frac{24}{7}$；第二种情况：如图5和图6，过P的直线与A、B共圆，作一个角与∠ABC相等，求此时x的最大值为$\frac{18}{7}$；由此写出x的取值范围．

解答 解：（1）如图1，△DEC∽△BAC，理由是：
∵A、B、E、D四点共圆，
∴∠EDC=∠B，
∵∠C=∠C，
∴△DEC∽△BAC；
（2）如图2，过P作PD⊥AB于D，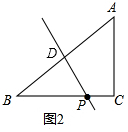
∴∠ADP=90°，
∵∠C=90°，
∴∠ADP+∠C=180°，
∴A、D、P、C四点共圆，
∴直线PD就是△ABC的共圆线，
在Rt△ABC中，AB=5，AC=3，
由勾股定理得：BC=4，
∴BP=BC-PC=4-1=3，
∵∠BDP=∠C=90°，∠B=∠B，
∴△BDP∽△BCA，
∴$\frac{BD}{BC}=\frac{BP}{AB}$，
∴$\frac{BD}{4}=\frac{3}{5}$，
∴BD=$\frac{12}{5}$，
∴AD=5-$\frac{12}{5}$=$\frac{13}{5}$；
（3）过A作AD⊥BC于D，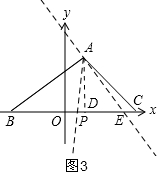
∵A（1，3），C（4，0），
∴AD=3，CD=4-1=3，
∴△ADC是等腰直角三角形，
∴∠ACD=45°，
过A作AE⊥AB，交AC于E，作∠BAE的平分线AP，交x轴于P，
∵∠DAE+∠DAB=90°，∠DAE+∠AED=90°，
∴∠DAB=∠AED，
∵∠ADB=∠ADE=90°，
∴△ADE∽△BDA，
∴$\frac{AD}{BD}=\frac{AE}{AB}$，
在Rt△ADB中，AD=3，BD=3+1=4$\sqrt{{5}^{2}+（\frac{15}{4}）^{2}}$，
∴AB=5，
∴$\frac{3}{4}=\frac{AE}{5}$，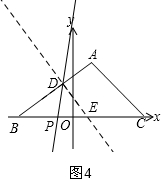
∴AE=$\frac{15}{4}$，
由勾股定理得：BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{5}^{2}+（\frac{15}{4}）^{2}}$=$\frac{25}{4}$，
∴EC=7-$\frac{25}{4}$=$\frac{3}{4}$，
∵AP平分∠BAE，
∴$\frac{AB}{AE}=\frac{BP}{PE}$，
∴$\frac{5}{\frac{15}{4}}$=$\frac{7-x}{x-\frac{3}{4}}$，
∴x=$\frac{24}{7}$；
如图4，在AB上任意取一点D作DE⊥AB，交BC于E，再作∠BDE的平分线，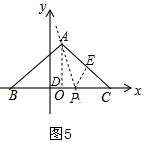
则∠BDE=90°，
∴∠BDP=45°，
∵∠ACD=45°，
∴∠ACD=∠BDP，
∴A、D、P、C四点共圆，
∴当$\frac{24}{7}$＜x＜7时，过P存在△ABC的共圆线，
如图5，作∠CAP=∠ABC，
∴△APE∽△BAD，
∵AD=3，BD=4，
∴设PE=3a，AE=4a，则EC=3a，AP=5a，
∴PC=3$\sqrt{2}$a，
∴PD=DC-PC=3-3$\sqrt{2}$a，
在Rt△APD中，${3}^{2}+（3-3\sqrt{2}a）^{2}=（5a）^{2}$，
7a²+18$\sqrt{2}$a-18=0，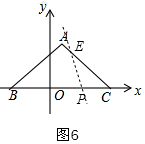
（a+3$\sqrt{2}$）（7a-3$\sqrt{2}$）=0，
a₁=-3$\sqrt{2}$（舍），a₂=$\frac{3\sqrt{2}}{7}$，
∴PC=3$\sqrt{2}$a=3$\sqrt{2}$×$\frac{3\sqrt{2}}{7}$=$\frac{18}{7}$，
如图6，同理作∠PEC=∠ABC，
则A、B、P、E四点共圆，
则当0＜x＜$\frac{18}{7}$时，过P存在△ABC的共圆线，
综上所述，当0＜x＜$\frac{18}{7}$和$\frac{24}{7}$＜x＜7时，过P存在△ABC的共圆线．

点评 本题主要考查了四点共圆的性质和判定，即：①共圆的四个点所连成的同侧共底的两个三角形的顶角相等；②圆内接四边形对角互补；③圆内接四边形的外角等于内对角；反之也成立．