
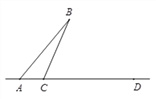
【题目】如图,线段AB,AD交于点A.C为直线AD上一点(不与点A,D重合).过点C在BC的右侧作射线CE⊥BC,过点D作直线DF∥AB,交CE于点G(G与D不重合).
(1)如图1,若点C在线段AD上,且∠BCA为钝角.
①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
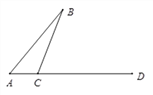
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系 ;
附加题(2分).
请你结合28题的题意提出一个新的拓展问题 .
【答案】(1)①补全图形如图. ②判断:∠CGD![]() ∠B=90°.证明见解析. (2) ∠CGD+∠B=90°.附加题参考:
∠B=90°.证明见解析. (2) ∠CGD+∠B=90°.附加题参考:
1.若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
2.若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
【解析】分析:(1) ①补全图形见解析;②先作辅助线,由∠2+∠HCG=180°和∠1+∠HCG=90°,推出结论∠CGD-∠B=90°即可;(2)由②中的结论可推导出结论∠CGD+∠B=90°. 附加题见解析.
解:(1)①补全图形如图:
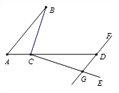
②判断:∠CGD-∠B=90°.
证明:过点C作CH∥AB,
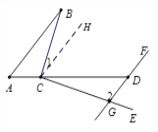
∴ ∠1=∠B(两直线平行,内错角相等).
∵ AB∥DF(已知),
∴ CH∥DF(平行于同一直线的两直线平行).
∴ ∠2+∠HCG=180°(两直线平行,同旁内角互补) .
∵ CE⊥BC(已知),
∴ ∠1+∠HCG=90°(垂直的定义).
∴ ∠CGD-∠B=90°.
(2) ∠CGD+∠B=90°.
附加题参考:
1.若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
2.若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
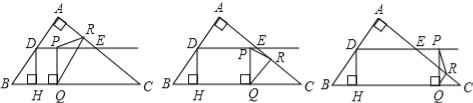
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)请根据统计图完成下列问题:

(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;条形统计图中,“很喜欢”月饼中喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中“很喜欢”月饼的有 人.
(3)李民同学最爱吃莲蓉月饼,陈丽同学最爱吃豆沙月饼,现有重量、包装完全一样的豆沙、莲蓉、蛋黄
三种月饼各一个,让李民、陈丽每人各选一个,则李民、陈丽两人都选中自己最爱吃的月饼的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2,则下列说法中不正确的是( )
A. 当a﹤5时,点B在⊙A内 B. 当1﹤a﹤5时,点B在⊙A内
C. 当a﹤-1时,点B在⊙A外 D. 当a﹥5时,点B在⊙A外
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
A. 点A在⊙O上 B. 点A在⊙O外
C. 点A在⊙O内 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )

A. ①② B. ③④ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com