
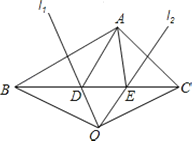
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
【答案】(1)线段BC的长为6cm;
(2)线段OA的长为5cm;
(3)∠DAE的度数为60°.
【解析】试题分析:(1)根据线段垂直平分线的性质得到DA=DB,EA=EC,根据三角形的周长公式计算即可;(2)根据线段垂直平分线的性质和三角形的周长公式计算即可;(3)根据线段垂直平分线的性质和等腰三角形的性质进行计算.
试题解析:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=6cm;
(2)

∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=16cm,
∴OA=0B=OC=5cm;
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC∠BAD∠EAC=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
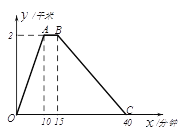
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多项式加上5x2﹣4x﹣3得﹣x2﹣3x,则这个多项式为( )
A. 4x2﹣7x﹣3 B. 6x2﹣x﹣3 C. ﹣6x2+x+3 D. ﹣6x2﹣7x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下面证明过程中的推理依据:
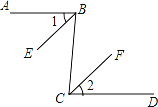
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.求证:∠1=∠2
证明:∵AB∥CD (__________)
∴∠ABC=∠BCD(__________)
∵BE平分∠ABC,CF平分∠BCD (__________)
∴∠1=![]() ∠ ______ ,(__________)
∠ ______ ,(__________)
∠2=![]() ∠ ______ .(__________)
∠ ______ .(__________)
∴∠1=∠2.(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冰箱冷冻室的温度为-6 ℃,此时房间内的温度为20 ℃,则房间内的温度比冰箱冷冻室的温度高( )
A. 26 ℃ B. 14 ℃ C. -26 ℃ D. -14 ℃
查看答案和解析>>
科目:初中数学 来源: 题型:
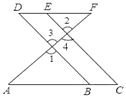
【题目】根据题意结合图形填空:如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2(已知)
且∠1=∠3______.
∴∠2=∠3(等量代换)
∴_________∥____________.
∴∠C=∠ABD__________________.
又∵∠C=∠D(已知)
∴_______________=______________(等量代换 )
∴AC∥DF__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com