
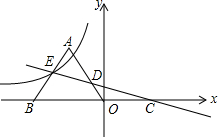
 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
分析 作EF⊥OB于F,AG⊥OB于G,设E(m,n),则OF=-m,EF=n,由于△OAB为等腰直角三角形,从而证得EF=BF=n,OB=-m+n,AG=$\frac{1}{2}$OB=$\frac{1}{2}$(-m+n),根据直线的解析式求得C的坐标,即可求得BC=-m+n+4,由S△AED=S△DOC得出S△EBC=S△ABO,从而得出$\frac{1}{2}$(-m+n)•$\frac{1}{2}$(-m+n)=$\frac{1}{2}$(-m+n+4)•n,整理得m2=n2+8n,由点E是直线y=-$\frac{1}{7}$x+$\frac{4}{7}$上的点,得出m=4-7n,代入m2=n2+8n化简得,3n2-4n+1=0,从而解得n=1,进而求得m=-3,得出E的坐标,代入反比例函数的解析式即可求得k的值.
解答 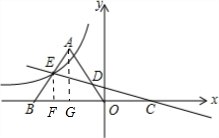 解:如图,作EF⊥OB于F,AG⊥OB于G,
解:如图,作EF⊥OB于F,AG⊥OB于G,
设E(m,n),
∴OF=-m,EF=n,
∵△OAB为等腰直角三角形,
∴∠ABO=45°,
∵EF⊥OB,
∴EF=BF=n,
∴OB=-m+n,
∴AG=$\frac{1}{2}$OB=$\frac{1}{2}$(-m+n),
∵一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与x轴交于C点,
∴C(4,0),
∴BC=-m+n+4,
∵S△AED=S△DOC,
∴S△EBC=S△ABO,
∴$\frac{1}{2}$OB•AG=$\frac{1}{2}$BC•EF,即$\frac{1}{2}$(-m+n)•$\frac{1}{2}$(-m+n)=$\frac{1}{2}$(-m+n+4)•n,
整理得,m2=n2+8n,
∵点E是直线y=-$\frac{1}{7}$x+$\frac{4}{7}$上的点,
∴n=-$\frac{1}{7}$m+$\frac{4}{7}$,得出m=4-7n,
代入m2=n2+8n化简得,3n2-4n+1=0
解得n=1或n=$\frac{1}{3}$,
∴m=-3或m=4-$\frac{7}{3}$>0(舍去),
∴E(-3,1),
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象过E点,
∴k=mn=-3.
故选C.
点评 本题考查了反比例函数和一次函数的交点问题,等腰直角三角形的性质,三角形面积,函数图象上点的坐标特征等,能够看出S△EBC=S△ABO是解题的关键.


科目:初中数学 来源: 题型:选择题
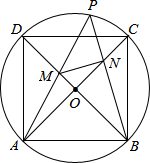 如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )
如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
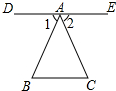 如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.
如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
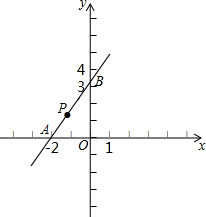 如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)
如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
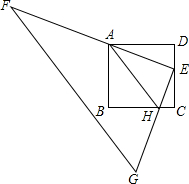 如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;
如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1.5,b=2,c=3 | B. | a=7,b=24,c=25 | C. | a=6,b=8,c=10 | D. | a=5,b=12,c=13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
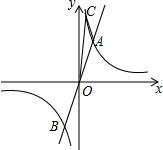 如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.
如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com