
【题目】关于二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.当![]() 时,
时,![]() 随
随![]() 的增大而减小B.它的图象与
的增大而减小B.它的图象与![]() 轴有交点
轴有交点
C.当![]() 时,
时,![]() D.它的图象与
D.它的图象与![]() 轴交于点
轴交于点![]()
【答案】C
【解析】
A. 根据对称轴及开口方向可判断;
B. 令y=0,解一元二次方程,可判断;
C. 通过抛物线与x轴的交点,结合开口方向可判断;
D. 令x=0,求出y值,可判断.
解:在函数y=x2-4x+3中a=1>0,
∴此函数图象开口向上;
又∵a=1,b=-4,c=3,
![]()
∴顶点坐标是(2,-1),且对称轴是x=2,
当x<1时,即说明x的取值范围在对称轴的左边,
∴y随x的增大而减小,故A正确,不符合题意;
∴令x2-4x+3=0,
解得x1=1,x2=3,
∴此函数图象和x轴有交点,求交点坐标是(1,0);(3,0).
故B正确,不符合题意;
当1<x<3时,抛物线在x轴下方,
∴y<0,故C错误,符合题意;
当x=0时,y=3,
∴抛物线与![]() 轴交于点
轴交于点![]() ,故D正确,不符合题意.
,故D正确,不符合题意.
故选:C.


科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
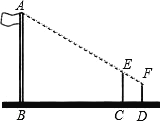
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数![]() (x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(x>0)的图像上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图像经过点A,与y轴的正半轴交于点B.
(1)求点A的坐标;
(2)若四边形ABOC的面积是![]() ,求一次函数y=kx+b的表达式.
,求一次函数y=kx+b的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD和正方形AEFG的边长分别为2和![]() ,点B在边AG上,点D在线段EA的延长线上,连接BE.
,点B在边AG上,点D在线段EA的延长线上,连接BE.
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
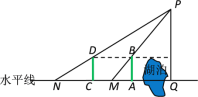
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com