练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

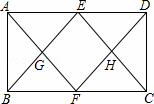
    如图，在矩形ABCD中，E，F分别为AD，BC的中点，连结AF，DF，BE，CE，AF与BE交于G，DF与CE交于H．求证：四边形EGFH为菱形．


                  证明：∵在矩形ABCD中AD=BC，且E、F分别是AD、BC的中点，

    ∴AE=DE=BF=CF

    又∵AD∥BC，

    ∴四边形AECF、BEDF是平行四边形．

    ∴GF∥EH、EG∥FH．

    ∴四边形EGFH是平行四边形．

    在△AEG和△FBG中，

    ，

    ∴△AEG≌△FBG（AAS）

    ∴EG=GB，AG=GF，

    在△ABE和△BAF中

    ∵，

    ∴△ABE≌△BAF（SAS），

    ∴AF=BE，

    ∵EG=GB=BE，AG=GF=AF，

    ∴EG=GF，

    ∴四边形EGFH是菱形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    准备一张矩形纸片，按如图操作：

    将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．

    （1）求证：四边形BFDE是平行四边形；

    （2）若四边形BFDE是菱形，AB=2，求菱形BFDE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一次数学测试中，小明所在小组6人的成绩（单位：分）分别为84、79、83、87、77、81，则这6人本次数学测试成绩的中位数是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若菱形的周长为20cm，则它的边长是　 　cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在▱ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF=BC，求证：四边形OCFE是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某林业部门要考查某种幼树在一定条件的移植成活率.在同样条件下，大量地对这种幼树进行移植，并统计成活情况，计算成活的频率．如下表：

    移植总数（n）

    成活数（m）

    成活的频率

    10

    8

    0.80

    50

    47

    0.94

    270

    235

    0.870

    400

    369

    0.923

    750

    662

    0.883

    1500

    1335

    0.89

    3500

    3203

    0.915

    7000

    6335

    0.905

    9000

    8073

    0.897

    14000

    12628

    0.902

    所以可以估计这种幼树移植成活的概率为

    （A）0.1                       （B）0.2                      （C）0.8                            （D）0.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知A（，y1），B（2，y2）为反比例函数图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP的长度之差达到最大时，点P的坐标是

    （A）（，0） （B）（1，0）

    （C）（，0） （D）（，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    太阳光线与地面成60°的角，照射在地面上的一只皮球上，皮球在地面上的投影长是，则皮球的直径是（　　）

    A．           B．15            C．10            D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，晚上，小亮在广场上乘凉．图中线段AB表示站在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯．

    （1）请你在图中画出小亮在照明灯（P）照射下的影子；

    （2）如果灯杆高PO=12m，小亮的身高AB=1.6m，小亮与灯杆的距离BO=13m，请求出小亮影子的长度．

    查看答案和解析>>

    同步练习册答案