
【题目】体育理化考试前夕,九(2)班组织了体育理化考试模拟(体育+理化=100分),模拟测试后相关负责人对成绩进行了统计,制作如下频数分布表和频数分布直方图,请根据表中信息解答问题:
分数段( | 频数 | 频率 |
| 5 | 0.1 |
| 5 |
|
|
| 0.4 |
| 15 | 0.3 |
| 5 | 0.1 |
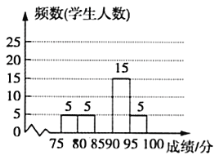
(1)表中![]() ________,
________,![]() ________,并补全直方图;
________,并补全直方图;
(2)若用扇形统计图描述此成绩分布情况,则分数段![]() 所对应扇形的圆心角度数是_____;
所对应扇形的圆心角度数是_____;
(3)若该校九年级共950名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?
【答案】(1)0.1;20;补图见详解;(2)108°;(3)665.
【解析】
(1)根据题意,5÷0.1=50可得九(2)班总人数,利用总人数,部分人数以及频率之间的关系,可求得相应的频率和部分人数即可;
(2)分数段![]() 所对应扇形的圆心角度数是360°×0.3计算即可;
所对应扇形的圆心角度数是360°×0.3计算即可;
(3)根据分数在![]() 中的频率,计算950×(0.3+0.4)即可.
中的频率,计算950×(0.3+0.4)即可.
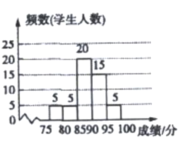
(1)由题意知,九(2)班总人数为5÷0.1=50(人),m=5÷50=0.1,n=50×0.4=20(人),补图如下:
故答案为:0.1;20;
(2)分数段![]() 所对应扇形的圆心角度数是360°×0.3=108°,
所对应扇形的圆心角度数是360°×0.3=108°,
故答案为:108°;
(3)估计该年级分数在![]() 的学生有950×(0.3+0.4)=665(人),
的学生有950×(0.3+0.4)=665(人),
答:估计该年级分数在![]() 的学生有665人,
的学生有665人,
故答案为:665.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
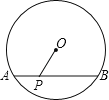
A.4个B.5个C.6个D.7个
查看答案和解析>>
科目:初中数学 来源: 题型:
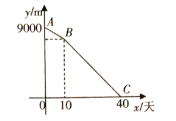
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
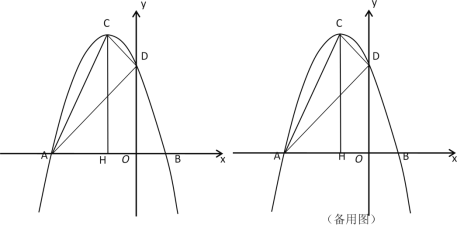
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
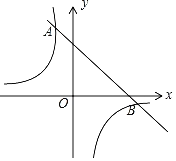
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足k1x+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
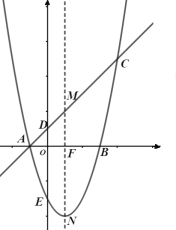
【题目】如图所示,平面直角坐标系中直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,点
两点,点![]() 坐标为
坐标为![]() .点
.点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交抛物线于点
,交抛物线于点![]() .
.

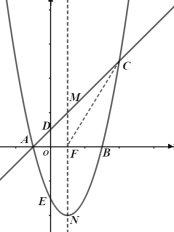
(1)求抛物线的解析式;
(2)是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,如果有,求点
为顶点的四边形为平行四边形,如果有,求点![]() 的坐标,如果没有,请说明理由;
的坐标,如果没有,请说明理由;
(3)若点![]() 在线段
在线段![]() 上移动时(不含端点),连接
上移动时(不含端点),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
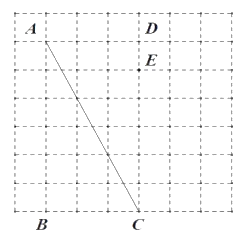
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形
的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形![]() 的顶点在格点上,点
的顶点在格点上,点![]() 是边
是边![]() 边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)①过![]() 作
作![]() 交
交![]() 边于
边于![]() ;
;
②过![]() 作
作![]() 于
于![]() 点;
点;
③在![]() 上作线段
上作线段![]()
(2)在(1)的条件下,连![]() ,若
,若![]() 为
为![]() 边上的动点,在网格中求作一条线段
边上的动点,在网格中求作一条线段![]() 等于
等于![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:

![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com