练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    阅读材料：一个边长为20cm正方形，按图1中的方法可以剪拼成一个底面是正方形的直四棱柱模型，且使它的表面积与原正方形面积相等．具体方法如下：沿粗黑实线剪下4个边长为5cm的小正方形，拼成一个正方形作为直四棱柱的一个底面；余下部分按虚线折叠成一个无盖直四棱柱；最后把两部分拼在一起，组成一个完整的直四棱柱．请按上述方法，将一个边长为20cm 的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型，使它的表面积与原正三角形的面积相等．
    要求：在图2中画出你的剪拼方法（用虚线表示要折叠的线，用粗黑实线表示要剪开的线），注出必要的数据，并给予简要说明．
    精英家教网
    分析：在正三角形的每一角上找出到顶点距离是5的点，然后作边的垂线，剪下后拼成一个正三角形，作为直三棱柱的一个底面即可．
    解答：解：如图2，沿黑线剪开，把剪下的三部分拼成一个正三角形，再沿虚线折叠即可．
    精英家教网
    点评：本题考查了图形的剪拼，解题的关键在于根据拼成棱柱的表面积与原图形的面积相等，从而判断出剪下的部分拼成的图形应该是棱柱的一个底面．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读下面材料：
    对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖．对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖．
    例如：图中①的三角形被一个圆覆盖，②中的四边形被两个圆所覆盖．
    回答下列问题：
    （1）边长为1cm的正方形被一个半径为r的圆所覆盖，r的最小值是
     
    cm；
    （2）边长为1cm的等边三角形被一个半径为r的圆所覆盖，r的最小值是
     
    cm；
    （3）长为2cm，宽为1cm的矩形被两个半径均为r的圆所覆盖，r的最小值是
     
    cm．这两个圆的圆心距是
     
    cm精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    请阅读下列材料：
    问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形，要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．
    小东同学的做法是：设新正方形的边长为x（x＞0），依题意，割补前后图形的面积相等，有x2=5，解得x=
    		5
    ，由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长，于是，画出如图②所示的分割线，拼出如图③所示的新正方形．精英家教网
    请你参考小东同学的做法，解决如下问题：
    现有10个边长为1的正方形，排列形式如图④，请把它们分割后拼接成一个新的正方形，要求：在图④中画出分割线，并在图⑤的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．（说明：直接画出图形，不要求写分析过程．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    77、阅读材料后再解答问题
    阿拉伯数学家阿尔•花拉子利用正方形图形巧妙解出了一元二次方程x2+2x-35=0的一个解．
    [阿尔．花拉子解法]将边长为xm的正方形和边长为1的正方形，外加两个长方形，长为x，宽为1，拼合在一起面积就是x2+2•x•1+1•1，而由x2+2x-35=0变形及x2+2x+1=35+1（如图所示）
    即左边边长为x+1的正方形面积为36．
    所以（x+1）2=36，则x=5．
    你能运用上述方法构造出符合方程x2+8x-9=0的一个正根的正方形吗？试一试吧!

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料，完成材料后问题

    课本上推导两个数和完全平方公式给出几何意义，利用图形的面积解释。

    如图1，一个边长为的正方形可以看做由

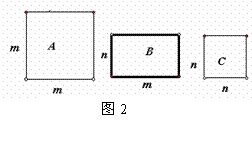    边长为的正方形和边长为的正方形以及长宽分别为的两个长方形构成。

    即边长为的正方形的面积有两种算法：以及，由此得到了一个等式： 。由此发现可以利用几何解释代数中的公式。请你参考课本上做法类比的解决下列问题：

    现有三种不同类型的长方形地砖长宽如图2所示。若现有A类4块，B类4块，C类2块，请问这些地砖的总面积为_______________________.如果用现有的地砖要拼成一个正方形，则多余1块___________型地砖（填A，B,C）；这样的地砖拼法也表示了一个两数和的平方的几何意义，请你用含有的等式写出这两个数的和的平方_________________，并类比阅读材料画图利用所给地砖，画图用图形面积给予几何直观的解释.

    查看答案和解析>>

    同步练习册答案