
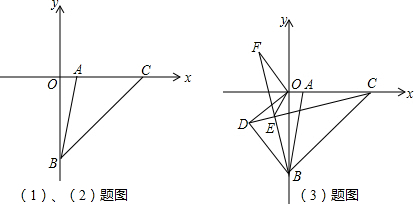
分析 (1)易求OC的长,即可求得AC的长,即可解题;
(2)作出图形,易证△PAM≌△BAO,可得PM=OB,AM=OA,即可解题;
(3)易证∠OCD=∠OBF和∠COD=∠BOF,即可证明△CDO≌△BFO,可得DO=FO,即可解题.
解答 解:(1)∵OC=5AO,AO=2,
∴OC=10,
∴AC=OC-OA=8,
∴S△ABC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×8×10=40;
(2)作出图形,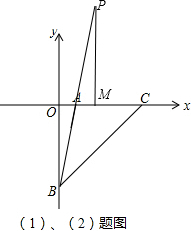
在△PAM和△BAO中,
$\left\{\begin{array}{l}{∠PMA=∠BOA=90°}\\{∠PAM=∠BAO}\\{PA=PB}\end{array}\right.$,
∴△PAM≌△BAO(AAS),
∴PM=OB=10,AM=OA=2,
∴点P坐标为(4,10);
(3)OD=OF,如图,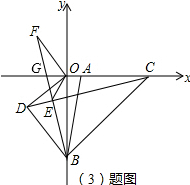
∵∠OCD+∠OGE=90°,∠OFE+∠OBF=90°,
∴∠OCD=∠OBF,
∵∠FOG+∠DOG=90°,∠DOG+∠BOD=90°,
∴∠BOD=∠FOG,
∵∠BOC=∠BOG=90°,
∴∠BOD+90°=∠FOG+90°,即∠COD=∠BOF,
在△CDO和△BFO中,$\left\{\begin{array}{l}{∠COD=∠BOF}\\{CO=BO}\\{∠OCD=∠OBF}\end{array}\right.$,
∴△CDO≌△BFO(ASA),
∴DO=FO,
∴当D点运动时,OD=OF.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△PAM≌△BAO和△CDO≌△BFO是解题的关键.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (xy)2÷(-xy)=-xy | B. | 4x4+2x4+x4=6x4 | C. | (-3mn)2=-6m2n2 | D. | (a-b)(-a-b)=a2-b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com