
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .

【答案】7.
【解析】
试题分析:过O作OF垂直于BC,再过A作AM垂直于OF,由四边形ABDE为正方形,得到OA=OB,∠AOB为直角,可得出两个角互余,再由AM垂直于MO,得到△AOM为直角三角形,其两个锐角互余,利用同角的余角相等可得出一对角相等,再由一对直角相等,OA=OB,利用AAS可得出△AOM与△BOF全等,由全等三角形的对应边相等可得出AM=OF,OM=FB,由三个角为直角的四边形为矩形得到ACFM为矩形,根据矩形的对边相等可得出AC=MF,AM=CF,等量代换可得出CF=OF,即△COF为等腰直角三角形,由斜边OC的长,利用勾股定理求出OF与CF的长,根据OF﹣MF求出OM的长,即为FB的长,由CF+FB即可求出BC的长.解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中,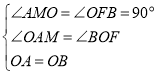 ,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6
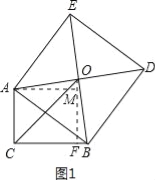
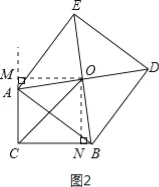
,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6![]() ,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6
,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6![]() ,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.
,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(3,-3),且与直线y=4x-3的交点B在x轴上.
(1)求直线AB对应的函数表达式;
(2)求直线AB与坐标轴所围成的三角形BOC(O为坐标原点,C为直线AB与y轴的交点)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假如在第34、35届奥运会上,中国代表团获得60枚金牌,这两届奥运会中国获得金牌之比是7:8,那么第35届奥运会中国代表团共获得了_____枚金牌.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A. 三角形的一个外角大于任何一个不相邻的内角
B. 三角形按边可分为不等边三角形、等腰三角形、等边三角形、
C. 三角形中最少有2个锐角
D. 三角形的三条中线交于一点,这个交点就是三角形的重心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点.
(1)在图①中以格点为顶点画一个三角形,使三角形三边长分别为2, ![]() ,
, ![]() ;
;
(2)在图②中以格点为顶点画一个面积为10的正方形;
(3)观察图③中带阴影的图形,请你将它适当剪开,重新拼成一个正方形(要求:在图③中用虚线作出,并用文字说明剪拼方法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的解题过程的横线上填空,并在括号内注明理由. 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:∵∠A=∠F(已知)
∴AC∥DF()
∴∠D=∠()
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE()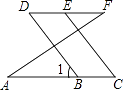
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com