
分析 (1)根据题意可以直接解答本题.
(2)由y1=y2,代入第一问中函数表达式,即可解得a的值.
(3)根据题目中给出的信息可以先求得点M、N的坐标,由题意可知点P在线段MN的垂直平分线上并且在抛物线上,从而可以求得点P的坐标.
解答 解:(1)∵m°n=mn(其中m,n是实数),y=x°(a°x+b)+2,
∴y=x(ax+b)+2=ax2+bx+2.
即:y=ax2+bx+2.
(2)∵当x=b-1时,y=y1;
当x=b+1时,y=y2;y1=y2,
∴a(b-1)2+b(b-1)+2=a(b+1)2+b(b+1)+2.
化简,得-2ab=b.
∴$a=-\frac{1}{2}$(b≠0).
(3)存在点P使得△PMN是等腰三角形.
理由:∵点(a,2ab+2)在直线y=kx+2上,
∴ka+2=2ab+2.
解得,k=2b.
∴直线y=2b+2.
又∵直线y=kx+2与函数y=x°(a°x+b)+2交于点M,N,
即直线y=2bx+2与函数y=ax2+bx+2交于点M,N,
∵点(0,2)在直线y=2bx+2和函数y=ax2+bx+2上,
∴设点M的坐标为(0,2),点N的坐标为(xn,yn),
∵∠MAN=90°,A点的坐标为(b,0),
∴$\frac{2}{0-b}×\frac{{y}_{n}}{{x}_{n}-b}=-1$…①
∵点N(xn,yn)在直线y=2bx+2上和函数y=ax2+bx+2上,其中a=-$\frac{1}{2}$,
∴yn=2bxn+2…②
${y}_{n}=-\frac{1}{2}{{x}_{n}}^{2}+b{x}_{n}+2$…③
由①②③可以解得,$b=\frac{2\sqrt{5}}{5},{x}_{n}=-\frac{4\sqrt{5}}{5},{y}_{n}=-\frac{6}{5}$或$b=-\frac{2\sqrt{5}}{5},{x}_{n}=\frac{4\sqrt{5}}{5},{y}_{n}=-\frac{6}{5}$.
函数y=-$\frac{1}{2}$x2+$\frac{2\sqrt{5}}{5}$x+2时,点N的坐标为($-\frac{4\sqrt{5}}{5},-\frac{6}{5}$);
函数y=-$\frac{1}{2}$${x}^{2}-\frac{2\sqrt{5}}{5}x$+2时,点N的坐标为($\frac{4\sqrt{5}}{5},-\frac{6}{5}$).
第一种情况:函数y=-$\frac{1}{2}$x2+$\frac{2\sqrt{5}}{5}$x+2时,点N的坐标为($-\frac{4\sqrt{5}}{5},-\frac{6}{5}$),点M的坐标为(0,2),设点P的坐标为(x,-$\frac{1}{2}$x2+$\frac{2\sqrt{5}}{5}$x+2),
则点P在线段MN的垂直平分线上,线段MN的中点坐标为($-\frac{2\sqrt{5}}{5},\frac{2}{5}$).
∴线段MN的垂直平分线为:y=$-\frac{4\sqrt{5}}{5}x-\frac{6}{5}$.
∵点P(x,-$\frac{1}{2}$x2+$\frac{2\sqrt{5}}{5}$x+2)在y=$-\frac{4\sqrt{5}}{5}x-\frac{6}{5}$上,
∴可得点P的坐标为:($\frac{6\sqrt{5}+2\sqrt{85}}{5},-\frac{30+8\sqrt{17}}{5}$)或($\frac{6\sqrt{5}-2\sqrt{85}}{5},-\frac{30-8\sqrt{17}}{5}$).
第二种情况:函数y=-$\frac{1}{2}$${x}^{2}-\frac{2\sqrt{5}}{5}x$+2时,点N的坐标为($\frac{4\sqrt{5}}{5},-\frac{6}{5}$),点M的坐标为(0,2),设点P的坐标为(x,-$\frac{1}{2}$${x}^{2}-\frac{2\sqrt{5}}{5}x$+2),
则点P在线段MN的垂直平分线上,线段MN的中点坐标为($\frac{2\sqrt{5}}{5},\frac{2}{5}$).
∴线段MN的垂直平分线为:y=$\frac{4\sqrt{5}}{5}x-\frac{6}{5}$.
∵点P(x,-$\frac{1}{2}$${x}^{2}-\frac{2\sqrt{5}}{5}x$+2)在y=$\frac{4\sqrt{5}}{5}x-\frac{6}{5}$上,
∴点P的坐标为:($\frac{-6\sqrt{5}+2\sqrt{85}}{5},\frac{-30+8\sqrt{17}}{5}$)或($\frac{-6\sqrt{5}-2\sqrt{85}}{5},\frac{-30-8\sqrt{17}}{5}$).
点评 本题考查对新定义的理解与应用、探究性问题、分类讨论的数学思想贯穿其中,解题的关键是分清题意,找出所求问题需要的条件,灵活变化,认真计算.


科目:初中数学 来源: 题型:选择题
| A. | 235 | B. | 216 | C. | 217 | D. | 208 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
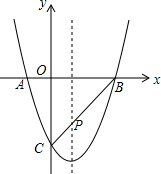 如图,已知二次函数y=ax2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于C点,且OB=OC,抛物线的对称轴交BC于点P.
如图,已知二次函数y=ax2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于C点,且OB=OC,抛物线的对称轴交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
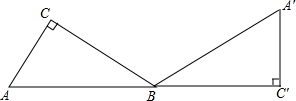 如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?
如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com